1. Запиши в стандартном виде многочлен. а) 5ay^3 + 7a^2 - 2a^3y + 6a^2 - ay^3 - 7a^2 =
б) 3c × 5d^2 + 6c × 2d^3 - cd^2 - 5cd^3

2. Продолжи запись:
а) степень многочлена 5x^6 - x^3 + 4x равна
б) степень многочлена 3x^4y^2 - 8x^2y + 2 равна
в) степень многочлена 26 + 3a равна
г) степень многочлена 3cd + ad - 8ac + 12 равна

3. Упрости выражение
а) 6,7a - (1,2a + 0,7a^3) =
б) (5,3x - x^2 + 8) + 0,5x^2 - (11,8x + 3,6x^2) =

ответ: Точка {9; 43}

Объяснение:

Чтобы найти точку минимума (ровно как и максимума) функции, необходимо взять производную от этой функции и приравнять ее к нулю. Сделаем это:

Мы получили две точки. Теперь нужно определиться, которая из них - точка минимума.

Для этого нарисуем на бумажке числовую прямую и отметим на ней получившиеся точки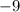 и .

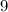Получим три промежутка:

Теперь для каждого из этих промежутков выберем какое-нибудь число и подставим его в производную, чтобы определить ее знак. Получим, что производная:

положительна на отрицательна на положительна на

Когда производная положительна на промежутке, функция возрастает, когда производная отрицательна - функция убывает.

Зарисовав соответствующие стрелочки под числовой прямой, получается, что функция имеет точку минимума в точке .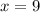

Осталось подставить ее в исходную функцию для нахождения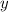 -координаты точки.

ОТВЕТ: 9;43

1.
(х - 2)² > x(x- 2)  
x²  - 4x +  4 > x²  - 2x
x² - 4x + 4  - x²  + 2x  > 0
-2x  + 4 > 0
- 2x  >  - 4      |  * ( - 1) ⇒ меняем знак неравенства
2x < 4
x < 2
неравенство верно при х∈( -∞ ; 2 )

а² + 1 ≥ 2(3a - 4)
a²  + 1 ≥ 6a  - 8
a²   +1  - 6а  + 8 ≥ 0
a²  - 6a + 9 ≥ 0
a² - 2*a*3 + 3²≥0
(a  - 3)²  ≥  0 
неравенство верно при всех значениях а (т.к. квадрат числа всегда больше 0 или равен 0 ) ⇒  а∈ ( -∞ ; +∞ )

2.
2,6 <√7 < 2,7           | * 2
5,2 <  2√7 < 5,4

2,6<√ 7 < 2,7           | * (-1) 
- 2,6 >  - √7 >  - 2,7
- 2,7 <  -√ 7 < - 2.6