1: Запишите уравнение, которые получатся, если обе части уравнения умножить на 4
2x-7y=11
Варианты ответа: −8x−28y=44 8x−28y=44 8x+28y=44 8x-28=11
2: Картинка
3:Картинка

​

Можно это сделать даже бе построения графиков. Для начала найдём вершину каждого из них и выясним направление ветвей параболы.
Знакомьтесь, это формула - х₀=(-в)/2а. Знакомо? Точно! Это формула похожа на формулу при решении квадратного уравнения, когда дискриминант равен нулю, не находишь? Это она и есть, ведь вершина - единственная точка параболы, значению х которой соответствует только одно значение у. Отсюда и формула. Ну, погнали...
Номер 1.
1) у=х²-6х+5 - парабола, ветви вверх.
2) х₀=(-(-6))/2*1=6/2=3
3) Так как ветви направлены вверх, то функция возрастает на промежутке [3;+∞) и убывает на промежутке (-∞;3]
Номер 2.
1) у=2х²-4х+5 - парабола, ветви вверх.
2) х₀=4/4=1
3) Функция возрастает на промежутке [1;+∞) и убывает на промежутке (-∞;1]
Номер 3. Попробуй решить сам, а потом сравни с решением ниже.
1) у=-х²+4х+1 - парабола, ветви ВНИЗ, так как коэффициент при квадрате отрицательный.
2) х₀=(-4)/(-2)=2
3) Функция возрастает на промежутке (-∞;2] и убывает на промежутке [2;+∞).

ответ: 1.5 часа.

Объяснение:

учить все квадраты совсем нет необходимости... в редкой задаче встречаются квадраты чисел, больших 25

достаточно грамотно пользоваться формулами сокращенного умножения и приемами разложения на множители при вычислении дискриминанта и корни будут "извлекаться сами"...

ведь если уравнение квадратное,

то для решения или т.Виета (устно) или дискриминант))

за t обозначим время, которое нужно найти;

тогда путь S₂ = 27 км, время t,

скорость на этом участке пути v₂ = S₂/t = 27/t

путь S₁ = 67-27 = 40 км, время 4-t,

скорость на этом участке пути v₁ = S₁/t = 40/(4-t)

получили уравнение: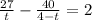

2t*(4-t) = 108-67t

2t² - 75t + 108 = 0

D = 75*75-4*2*108 = 9*25*25-8*4*27=9*(625-96)=(3*23)²

t₁ = (75+69)/4 = 144/4 > 4 часов--посторонний корень

t₂ = (75-69)/4 = 6/4 = 3/2 = 1.5