ну графики ты сама построишь если умеешь строить графики линейных функций
а находить координаты пересечений без графика надо с системы
y=-4x+1 { - объединение в систему функций
{
y=2x-3 |вторую функцию умножаем на 2 чтобы решить путём сложения
y=-4x+1
2y=4x-6 умножаем 2 функцию yf 2 для решения путём сложения -4x и 4x сокращаются
3y=-5
y=-5/3 (дробь впереди со знаком -)
подставляем значение y в любую из фукций системы например в 1 и решаем
-5/3=-4x+1
4x-1=5/3
4x=8/3
x=2/3
для проверки попробуем подставить во вторую функцию
-5/3=2x-3
-2x+3=5/3
-2x=-4/3
точка пересечения (2/3; -5/3)
надеюсь в задаче те надо было найти точку пересечения без графиков
Здравствуйте, Sonya2006f!
Чтобы восстановить неполный квадрат суммы, нужно представить крайние члены данной формулы в виде числа со степенью.
Разложение чисел на простые множители:
Теперь когда мы знаем, как представить данные члены в виде числа со степенью, запишем формулу, по которой выполнялось разложение.
Формула сокращённого умножения:
НЕПОЛНЫЙ КВАДРАТ СУММЫ: .
Зная, что первоначально выражение имело вид , перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.
Разложение данного выражения на множители:
Окончательный ответ данной задачи:
Неполный квадрат суммы данного выражения - "6x".
С Уважением, NeNs07.
ну графики ты сама построишь если умеешь строить графики линейных функций
а находить координаты пересечений без графика надо с системы
y=-4x+1 { - объединение в систему функций
{
y=2x-3 |вторую функцию умножаем на 2 чтобы решить путём сложения
y=-4x+1
{
2y=4x-6 умножаем 2 функцию yf 2 для решения путём сложения -4x и 4x сокращаются
3y=-5
y=-5/3 (дробь впереди со знаком -)
подставляем значение y в любую из фукций системы например в 1 и решаем
-5/3=-4x+1
4x-1=5/3
4x=8/3
x=2/3
для проверки попробуем подставить во вторую функцию
-5/3=2x-3
-2x+3=5/3
-2x=-4/3
x=2/3
точка пересечения (2/3; -5/3)
надеюсь в задаче те надо было найти точку пересечения без графиков
Здравствуйте, Sonya2006f!
Чтобы восстановить неполный квадрат суммы, нужно представить крайние члены данной формулы в виде числа со степенью.
Разложение чисел на простые множители:
Теперь когда мы знаем, как представить данные члены в виде числа со степенью, запишем формулу, по которой выполнялось разложение.
Формула сокращённого умножения:
НЕПОЛНЫЙ КВАДРАТ СУММЫ: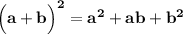
.
Зная, что первоначально выражение имело вид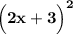
, перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.
Разложение данного выражения на множители:
Окончательный ответ данной задачи:
Неполный квадрат суммы данного выражения - "6x".
С Уважением, NeNs07.