Принцип такой, что в горизонтальной и вертикальной линиях должно быть столько камушков, какой номер у уголка.
То есть, в 6 уголке должно быть 6 по вертикали и 6 по горизонтали, один из которых (на стыке) общий камушек. Таким образом, мы можем узнать количество камушков в любом по счету уголке.
Формула:
Где n - номер уголка
В шестом уголке:
В уголке n:
В первых двух уголках камушков:
В первых пяти уголках.
Видим, что с каждым номером количество камушков становится на два больше (потому что мы прибавляем один камушек в горизонтальную линию и один в вертикальную.
Тогда в первых пяти уголках камушков будет:
Заметим, что если считать все камушки по порядку с первого до пятого, то число камушков во всех этих уголках равно квадрату номера последнего уголка.
x = 7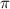 /6
/6
Объяснение:
2 sin x = -1
sin x = -0.5
Отмечаем нужные точки на тригонометрическом круге
Это x = -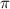 /6 + 2
/6 + 2
Так же можно задать это множество решений так:
x =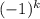 * (-
* (-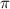 /6) +
/6) +
Нам нужно выбрать из множества решений только те, которые принадлежат заданному промежутку.
Отметим этот промежуток на тригонометрическом круге
Из рисунка видно, что подходит только одно решение x = 7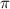 /6
/6
Это решение можно было найти другим решив неравенство
1/2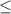 7/6 + 2k
7/6 + 2k
3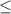 7 + 12k
7 + 12k
Так как k - целое, то подходит только k = 0, при других целых k неравенство не выполняется.
1/2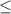 -1/6 + 2k
-1/6 + 2k
3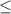 -1 + 12k
-1 + 12k
Здесь нет целых значений k, для которых бы выполнялось неравенство (при k = 0 -1+0<3, при k = 1 -1+11>9)
Значит, решением является только x = 7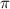 /6
/6
Но здесь проще находить решение именно из тригонометрического круга по рисунку.
В третьем уголке 5 камешков.
Принцип такой, что в горизонтальной и вертикальной линиях должно быть столько камушков, какой номер у уголка.
То есть, в 6 уголке должно быть 6 по вертикали и 6 по горизонтали, один из которых (на стыке) общий камушек. Таким образом, мы можем узнать количество камушков в любом по счету уголке.
Формула:
Где n - номер уголка
В шестом уголке:
В уголке n:
В первых двух уголках камушков:
В первых пяти уголках.
Видим, что с каждым номером количество камушков становится на два больше (потому что мы прибавляем один камушек в горизонтальную линию и один в вертикальную.
Тогда в первых пяти уголках камушков будет:
Заметим, что если считать все камушки по порядку с первого до пятого, то число камушков во всех этих уголках равно квадрату номера последнего уголка.
Для трех уголков:
Для четырех:
Значит, для 100 камушков