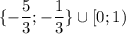10. Петя — любитель математики — во время прогулок, складывая четырёхзначный номер проезжающего автомобиля с числом, образованными
теми же цифрами, но в обратном порядке, нашёл наибольший общий делитель
всех полученных сумм. Чему он равен?
А. 11. Б. 101. В. 110. Г. 111.
Реши задачи и запиши их полные решения
11. В семье моего товарища произведение возрастов двух детей, сейчас
равно возрасту их отца. Может ли это произойти и через несколько лет?
(возраст — это целое число полностью прожитых лет).
12. В школе 5 шестых классов. Может ли так быть, что в 6-А и 6-Б вместе
27 учащихся, в 6-Б и 6-В — 39, в 6-В и 6-Г — 57, в 6-Г и 6-Б Д — 33, в 6-Д и 6-
А — 48 учащихся?

Показать ответ

Ответ:

danul1414

29.08.2020 23:12

Abc с чертой вверху ---это запись трехзначного числа...
например, 367 и тогда a=3, b=6, c=7
a --- количество сотен, в выражении запишется как 100*а
b --- количество десятков, в выражении запишется как 10*b
c --- количество единиц, в выражении запишется как 1*с
итак, abc(черта вверху) + cab(черта вверху) =
= 100a + 10b + с + 100с + 10а + b = 100*(a+c) + 10*(a+b) + b+c
2)
15 в любой степени закончится цифрой 5 (т.к. 5*5 = 25)
26 в любой степени закончится цифрой 6 (т.к. 6*6 = 36)
39 в четной степени закончится цифрой 1 (т.к. 9*9 = 81)
в нечетной степени закончится цифрой 9 (т.к. 9*1 = 9)
а) сумма заканчивается цифрой 0 (т.к. 5+6+9 = 20)
б) 99⁹ (в нечетной степени) закончится на 9, т.е. получится вновь нечетный показатель степени
и 99 с нечетным показателем степени закончится на 9

0,0(0 оценок)

Ответ:

xandar815

18.07.2022 03:27

Рассмотрим первое уравнение:

$\displaystyle y(y-7)=xy-5(x+2)\\y^2-7y-xy+5x+10=0\\y^2-7y+10-xy+5x=0\\(y-2)(y-5)-x(y-5)=0\\(y-5)(y-x-2)=0\\\left [ {{y=5} \atop {y=x+2}} \right.$

Можно построить этот график. Учитывая неравенство, строим до прямой x = 6.

Рассмотрим второе уравнение:

$\displaystyle\frac{a(x-6)-2}{y-2}=1\\\left \{ {{a(x-6)-2=y-2} \atop {y\neq 2}} \right. \\\left \{ {{y=a(x-6)} \atop {y\neq 2}} \right.$

График этого уравнения — прямая, проходящая через точку (6; 0) с меняющимся углом наклона. Причём из него же следует, что точку с y = 2 можно выколоть на графике первого уравнения.

График первого уравнения начерчен красным цветом, вариации второго — зелёным.

Возьмём a = 0 и будем увеличивать угол наклона. До a = 1 будет ровно одно пересечение. При a ≥ 1 прямая либо будет параллельна прямой y = x + 2, либо не будет иметь пересечений.

Если уменьшать угол наклона, то при отрицательных a будет два решения, за исключением случаев, когда прямая проходит через выколотую точку (0; 2) и "общую" точку (3; 5):