Исследуем функцию на ее области определения: x є (1/e; +∞).
Слева имеем постоянную функцию, справа - монотонно возрастающую на области определения, поэтому уравнение имеет не более одного решения. Очевидно, что x = 1 - корень уравнения, а также - критическая точка функции
Вычислим знаки производной на интервалах (1/e; 1) и (1; +∞): возьмем, к примеру, числа 1/2 и e.
Имеем: , т.к. 1 - 2e < 0.
А из этого следует что числитель дроби положителен, что можно сказать и про знаменатель. Тогда f'(0,5)>0
Т.к. на интервале (1/e; 1) f'(x) > 0 , а на интервале (1; +∞) f'(x) < 0, x = 1 - точка максимума. Найдем значение максимума:\
Т.е. максимум равен f(1) = 0. Уже очевидно, что других корней уравнение иметь не будет, т.к. ни при каких других x максимум - 0 - достигаться не будет. А значит единственный корень уравнения - x = 1.
Число по определению десятичной записи представимо в виде . Точно также, например, , и т. д.
В задаче 24 получаем уравнение:
Поскольку и цифры двузначного числа, то .
Чтобы выполнилось последнее равенство, надо найти общее кратное чисел 8 и 3. В данном случае найдём НОК(8,3), которое равно 24. Тогда а=3, b=8, а сумма a+b=11. Можно легко перебрать из неравенства, что других решений нет (если взять какое-нибудь большее кратное, то a или b станет больше девяти).
***
Вторая задача решается точно так же. Дам решение уже без объяснений.
Исследуем функцию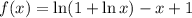
на ее области определения: x є (1/e; +∞).
Слева имеем постоянную функцию, справа - монотонно возрастающую на области определения, поэтому уравнение имеет не более одного решения. Очевидно, что x = 1 - корень уравнения, а также - критическая точка функции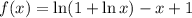
Вычислим знаки производной на интервалах (1/e; 1) и (1; +∞): возьмем, к примеру, числа 1/2 и e.
Имеем: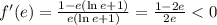
, т.к. 1 - 2e < 0.
А из этого следует что числитель дроби положителен, что можно сказать и про знаменатель. Тогда f'(0,5)>0
Т.к. на интервале (1/e; 1) f'(x) > 0 , а на интервале (1; +∞) f'(x) < 0, x = 1 - точка максимума. Найдем значение максимума:\
Т.е. максимум равен f(1) = 0. Уже очевидно, что других корней уравнение иметь не будет, т.к. ни при каких других x максимум - 0 - достигаться не будет. А значит единственный корень уравнения - x = 1.
ОТВЕТ: x = 1
Число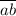
по определению десятичной записи представимо в виде 
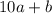. Точно также, например, 
, 
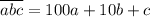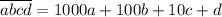и т. д.
В задаче 24 получаем уравнение:
Поскольку
и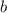 
цифры двузначного числа, то 
.
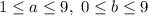Чтобы выполнилось последнее равенство, надо найти общее кратное чисел 8 и 3. В данном случае найдём НОК(8,3), которое равно 24. Тогда а=3, b=8, а сумма a+b=11. Можно легко перебрать из неравенства, что других решений нет (если взять какое-нибудь большее кратное, то a или b станет больше девяти).
***
Вторая задача решается точно так же. Дам решение уже без объяснений.