11 класс не знаю как решить

Во Укажите величину, не являющуюся скалярной
Варианты ответов
длина отрезка
площадь фигуры
Работа силы
Масса

Во Вектор может быть задан
Варианты ответов
Только длиной
Координатами начала
Точкой приложения
Длиной и направлением

Во Вектор
а
(0;1;0) лежит на оси:
Варианты ответов
Абсцис
Апплика
Ординат
В начале координат

Во Вектор
а
(0;0;1) является
Варианты ответов
Нулевым
Правильным
Неправильным
Единичным

Во Вектор
В
А
задан координатами начала и конца, т.е. А(-2;-1;8), В(1;3;-5), тогда он имеет координаты:
Варианты ответов
(3;4;-13)
(-1;2;-13
(-3;-4;13
(-3;-4;3)

Во Квадрат длины вектора
а
(-2;5;1) равен:
Варианты ответов
30
16
4
-8

Показать ответ

Ответ:

Abdueva

07.09.2020 01:42

Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.

1-ое свойство, которое понадобится

$a+c \equiv b + d \ (mod \ m)$

То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.

2-ое свойство, которое нам понадобится:

$ac \equiv bd \ (mod \ m)$

То есть довольно аналогичная вещь в произведении

На нашем примере все увидим

$a = 5\cdot 2^{51}+21\cdot 32^{45}$

Находим остатки по модулю 31

Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,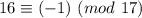 $16 \equiv (-1) \ (mod \ 17)$ , но сейчас это не нужно), нам повезло, это 32

Учитываем, что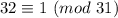 $32 \equiv 1 \ (mod \ 31)$ , получаем

$5\cdot 2^{51} = 5\cdot 2^1 \cdot 2^{50}=10 \cdot 2^{10\cdot 5} = 10 \cdot (2^{5})^{10}= 10\cdot 32^{10} \equiv 10 \cdot 1^{10} \ (mod \ 31)$

То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым

$21\cdot 32^{45} \equiv 21 \cdot 1^{45}\ (mod \ 31) \equiv 21 \ (mod \ 31)$

Остаток 21, чудесно. Выполняем последний шаг.

$5\cdot 2^{51}+21\cdot 32^{45} \equiv 10+21 \ (mod \ 31) \equiv 31 \ (mod \ 31) \equiv 0 \ (mod \ 31)$

То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.

0,0(0 оценок)

Ответ:

YAMAHAv

24.05.2021 21:28

Область допустимых значений (ОДЗ): x >= -4.
x - 4*V(x + 4) - 1 < 0 ( V - корень квадратный).
x - 1 < 4*V(x + 4)
Правая часть неравенства <= 0 для всех х из ОДЗ, левая часть < 0 при x < 1, то есть неравенство выполняется при x < 1,
с учетом ОДЗ получаем -4 <= х < 1.
Пусть x >= 1.
Возведем обе части неравенства в квадрат
(x - 1)^2 < 16*(x + 4)
x^2 - 2*x + 1 < 16*x + 64
x^2 - 18*x - 63 < 0
Равенство верно на интервале между корнями уравнения.
Корни х1 = -3, х2 = 21, неравенство выполняется для -3 < х < 21, с учетом x >= 1 получаем 1 <= х < 21.
Объединяем условия -4 <= х < 1 и 1 <= х < 21, получаем
ответ: -4 <= х < 21.

0,0(0 оценок)

Популярные вопросы: Алгебра