(11-x/2)^90 tg^4(4x-x^2) уравнение касательной и нормали к графику функции в данной точке f(x)=2x-x^2,x=1 f(x)=sin x,x=п/4 надо просто ну сильно - не допускают к сессии!

Показать ответ

Ответ:

danilkuzin201

17.06.2020 13:44

$1)\quad f'(x)=2-2x$

Уравнение касательной имеет вид

y=f'(1)(x-1)+f(1)

y=(2-2*1)*(x-1)+(2*1-1^2)

y=1

Уравнение нормали будет перпендикулярно уравнению касательной в данной точке.

В данном случае будет иметь вид х=1. Так как эта прямая перпендикулярна касательной в точке х=1 прямой у=1.

$2)\quad f'(x)=\cos x$

Уравнение касательной имеет вид

$y=f'(\frac{\pi}{4})*(x-\frac{\pi}{4})+\sin\frac{\pi}{4}$

$y=\frac{\sqrt{2}}{2}*(x-\frac{\pi}{4})+\frac{\sqrt{2}}{2}$

$y=\frac{\sqrt{2}}{2}*x-\frac{\sqrt{2}\pi}{8}+\frac{\sqrt{2}}{2}$ - это будет уравнение касательной.

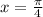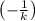
Чтобы найти уравнение нормали надо взять прямую, перпендикулярную данной в точке $x=\frac{\pi}{4}$ . Угловой коэффициент у такой прямой будет отличаться от исходной прямой тем, что будет равен $\left(-\frac{1}{k}\right)$

В данном случае прямая будет иметь вид

$y=-\frac{1}{\frac{\sqrt{2}}{2}}x+b$

Или

$y=-\sqrt{2}x+b\quad(*)$

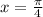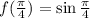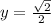Так как проходит через точку $x=\frac{\pi}{4}$ и значение нормали равно значению самой исходной функции, то есть $f(\frac{\pi}{4})=\sin\frac{\pi}{4}$ , то есть $y=\frac{\sqrt{2}}{2}$ . Подставим эти значения в уравнение (*).