Понимаем, что график не даст нам точные координаты пересечения и строим его схематически (см рис.)
2) Одна точка пересечения (-2; -5) (пересечение прямых x = - 2 и y = -5).
Найдем две точки пересечения:
5x + 2y = 10 и x = -2 ⇒ -10 + 2y = 10 ⇒ y = 10 ⇒ (-2; 10)
5x + 2y = 10 и y = -5 ⇒ 5x - 10 = 10 ⇒ x = 4 ⇒ (4; -5)
Т.к. один из углов треугольника образован пересечением перпендикулярных прямых x = - 2 и y = -5, то он прямоугольный и можем найти длину катетов, вычитая ординаты точек для пары (-2; -5) и (-2; 10) ⇒ a = 10 - (-5) = 15
и абсциссы точек для пары (-2; -5) и (4; -5) ⇒ b = 4 - (-2) = 6
Тогда
Для более общего решения найдем площадь треугольника заданного координатами трех точек в двухмерном декартовом пространстве как половину векторного произведения построенного на двух векторах задающих две стороны треугольника.
Для треугольника построенного на точках площадь будет равна:
Сложение рациональных чисел обладает переместительным и сочетательным свойствами. Иными словами, если а , b и c — любые рациональные числа, то а + b = b + а , а + (b + с) = (а + b) + с .
Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю. Значит, для любого рационального числа имеем: а + 0 = а , а + (– а) = 0 .
Умножение рациональных чисел обладает переместительным и сочетательным свойствами. Если, а , b и c рациональные числа, то:
ab = ba , a(bc) = (ab)c . Умножение на 1 не изменяет рационального числа, а произведение числа на обратное ему число равно 1 . Значит, для любого рационального числа а имеем:
а • 1 = а ;
Умножение числа на нуль дает в произведении нуль, т. е. для любого рационального числа а имеем:
а • 0 = 0 ; Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю:
если а • b = 0 , то либо а = 0 , либо b = 0 (может случиться, что и а = 0 , и b = 0 ) . Умножение рациональных чисел обладает и распределительным свойством относительно сложения. Другими словами, для любых рациональных чисел а , b и c имеем:
1) Решим систему, чтобы облегчить построение:
Понимаем, что график не даст нам точные координаты пересечения и строим его схематически (см рис.)
2) Одна точка пересечения (-2; -5) (пересечение прямых x = - 2 и y = -5).
Найдем две точки пересечения:
5x + 2y = 10 и x = -2 ⇒ -10 + 2y = 10 ⇒ y = 10 ⇒ (-2; 10)
5x + 2y = 10 и y = -5 ⇒ 5x - 10 = 10 ⇒ x = 4 ⇒ (4; -5)
Т.к. один из углов треугольника образован пересечением перпендикулярных прямых x = - 2 и y = -5, то он прямоугольный и можем найти длину катетов, вычитая ординаты точек для пары (-2; -5) и (-2; 10) ⇒ a = 10 - (-5) = 15
и абсциссы точек для пары (-2; -5) и (4; -5) ⇒ b = 4 - (-2) = 6
Тогда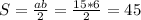
Для более общего решения найдем площадь треугольника заданного координатами трех точек в двухмерном декартовом пространстве как половину векторного произведения построенного на двух векторах задающих две стороны треугольника.
Для треугольника построенного на точках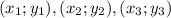
площадь будет равна:
а + b = b + а , а + (b + с) = (а + b) + с .
Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю. Значит, для любого рационального числа имеем:
а + 0 = а , а + (– а) = 0 .
Умножение рациональных чисел обладает переместительным и сочетательным свойствами. Если, а , b и c рациональные числа, то:
ab = ba , a(bc) = (ab)c .
Умножение на 1 не изменяет рационального числа, а произведение числа на обратное ему число равно 1 . Значит, для любого рационального числа а имеем:
а • 1 = а ;
Умножение числа на нуль дает в произведении нуль, т. е. для любого рационального числа а имеем:
а • 0 = 0 ;
Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю:
если а • b = 0 , то либо а = 0 , либо b = 0
(может случиться, что и а = 0 , и b = 0 ) .
Умножение рациональных чисел обладает и распределительным свойством относительно сложения. Другими словами, для любых рациональных чисел а , b и c имеем:
(а + b)с = ас + bс.