14.5. найдите разность арифметической прогрессии (а
1) а = 18, n = 27, s. – 2241; 2) а. - -8, п = 17, s.
3) а = -5, n = 23, s = 1909; 4) а = 81, n = 34.
от 90 йилен и значение суммы 20 первых членов
81. n = 34, s = 510.
20 ​

х∈(3, 4).

Объяснение:

Решить систему неравенств:

х>3

4-х>0

Первое неравенство:

х>3

Решения неравенства находятся в интервале от х=3 до + бесконечности.

х∈(3, +∞), это решение первого неравенства.

Неравенство строгое, скобки круглые.

Второе неравенство:

4-х>0

-x>-4

x<4  знак меняется

Решения неравенства находятся в интервале при х от  - бесконечности до 4.

х∈(-∞, 4), это решение второго неравенства.

Неравенство строгое, скобки круглые.

Теперь нужно на числовой оси отметить оба интервала, чтобы найти пересечение, то есть, такое решение, которое подходит двум неравенствам.

Чертим числовую ось, отмечаем точки 3 и 4. Штриховка от точки 3 вправо до + бесконечности, от 4 влево до - бесконечности.

Пересечение х∈(3, 4), это и есть решение системы неравенств.

Объяснение:

Рассмотрим сначала первое неравенство системы.

Начнем с ОДЗ:

Продолжим решение:

1)

Замена: .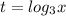

Обратная замена:

С учетом ОДЗ оба корня подходят.

2)

С учетом ОДЗ получим, что решение неравенства:

Теперь перейдем ко второму неравенству системы:

Понятно, что сначала нужно написать ОДЗ.

Продолжим решение:

Заметим, что данное неравенство хорошо раскладывается на множители:

Решим неравенство по методу интервалов.

1)

2)

Введем функци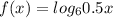и и 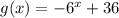. Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, 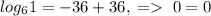, верно. Так, мы решили это уравнение, получив, что его корень x=2.

Тогда решение неравенства с учетом ОДЗ:

Итого имеем:

Найдем пересечение:

Задание выполнено!