(см. объяснение)
Объяснение:
Так как не является корнем уравнения, то поделим его на :
Выполним замену вида .
Тогда получим уравнение:
По формуле Кардано:
Обратная замена:
Решая это уравнение, получаем ответ:
Уравнение решено!
(см. объяснение)
Объяснение:
Так как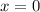 не является корнем уравнения, то поделим его на
не является корнем уравнения, то поделим его на  :
:
Выполним замену вида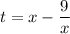 .
.
Тогда получим уравнение:
По формуле Кардано:
Обратная замена:
Решая это уравнение, получаем ответ:
Уравнение решено!