144. Разложите на множители: 1) 11т* -11;
6) -8° + 8a3 - 2а:
2) 6a3 - 6а;
7) 5а – 40b6,
3) 5х3 – 5xy”,
4) 8a2ъ2 – 72а22,
5) 2x2 +24xy +72у2;
8) а3 - ab-a®ь +а",
9) а – 3Ь +а2 – 9ь 2.
10) ас-с-ас? +2.
145. Разложите на множители:
1) х2 + 2xy +y2 -49;
т
2) а” - 9ь? + 6bc-c2;
5) +6 – 464 +1262 — 9;
6) m3 + 27n3+m° + бmn + 9n;
7) а2 + 2ab+b2-c2+4cd-4d2.
3) x°у? – ху — х3 +х;
4) а3 + 8-а? – 2а;
8) а2 -2 + 4а +4.
146. Решите уравнение:​

Объяснение:

Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.

Значит у подобного треугольника стороны тоже относятся  как 2: 5:7.

2+5+7=14 частей всего

84:14= 6 см будет одна часть

6*2=12 см это первая сторона треугольника

6*5=30 см это вторая сторона треугольника

6*7=42 см это третья сторона треугольника

только с данными сторонами нельзя построить треугольник,потому что

каждая сторона треугольника должна быть меньше суммы двух других  сторон . а  здесь 42 =30+12.

Объяснение:

1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.

В примере в) коэффициенты k=5, значит их графики параллельны.

2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.

3. АБВГ

2413

4. 2x + y = 8

2x - y = 1

Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:

2x - (8 - 2x) = 1

2x - 8 + 2x = 1

4x = 9

x = 2,25

y = 8 - 2*2,25 = 8 - 4,5 = 3,5

ответ: (2,25; 3,5)

5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.

2)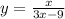 . Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.

б)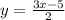 при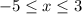

Если x = -5, то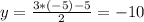

Если х= 3, то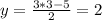

Значит,