15:46 50 Х Online Mektep - BilimLand onlinemektep.org х Табиғат сипаты. Не жауып тұр. Қастек Баянбай Үзіндіні мәнерлеп оқу үшін қойылған шартты белгі мағынасын анықта. Тегін аққA жұрт карық болатынДАй бір ауық. Нұр жауып тұр, Нұр жауып! — Деді әпкем жымиып. белгіленген дыбыстарға екпін түсіріп айту белгіленген дыбыстарға екпін түсірмей айту өзгеріссіз айту Тексеру Артқа
В слове ИНСТИТУТ 8 букв, но среди них есть повторяющиеся буквы, а именно
И - 2 раза
Т - 3 раза
Тогда количетсво перестановки букв такое:
На первое место мы поставим одну из 8 букв
На второе - одну из 7 оставшихся
На третье - одну из 6 оставшихся
......
и так далее до 1.
Так как выбор одной буквы зависит от выбора других, то нам необходимо все перемножить
Но так как были повторяющиеся буквы, мы могли одну и ту же букву посчитать несколько раз, то нам необходимо посчитать количество перестановок всех повторяющихся букв, и поделить на их количество. так как считали мы их зря.
20(x²-6x-9)²=x(x²-4x-9) (x²-6x-9)²-x(x²-4x-9)=0 (x²-6x)²-2(x²-6x)·9+9²-x³+4x²+9x=0 x⁴-12x³+36x²-18x²+108x+81-x³+4x²+9x=0 x⁴-13x³+22x²+117x+81=0 подставив вместо х=-1 убеждаемся, что 1+13+22-117+81=0 - верно Значит х=-1 - корень данного уравнения Делим x⁴-13x³+22x²+117x+81 на (х+1) получим х³-14х²+36х+81 Итак, x⁴-13x³+22x²+117x+81=(х+1)·(х³-14х²+36х+81) корни многочлена х³-14х²+36х+81 следует искать среди делителей свободного коэффициента 81
Это числа ±1;±3;±9 Подставим х=9 и убеждаемся, что 9³-14·9²+36·9+81=81(9-14+4+1)=81·0=0 х=9 - корень данного уравнения х³-14х²+36х+81 делим на (х-9) получим х²-5х-9 Осталось разложить на множители последнее выражение х²-5х-9=0 D=25+36=61 x=(5-√61)/2 или х=(5+√61)/2
Окончательно x⁴-13x³+22x²+117x+81=0 ⇒(х+1)·(х³-14х²+36х+81)=0⇒(х+1)(х-9)(х²-5х-9)=0⇒ х₁=-1 или х₂=9 или x₃=(5-√61)/2 или х₄=(5+√61)/2
3360
Объяснение:
В слове ИНСТИТУТ 8 букв, но среди них есть повторяющиеся буквы, а именно
И - 2 раза
Т - 3 раза
Тогда количетсво перестановки букв такое:
На первое место мы поставим одну из 8 букв
На второе - одну из 7 оставшихся
На третье - одну из 6 оставшихся
......
и так далее до 1.
Так как выбор одной буквы зависит от выбора других, то нам необходимо все перемножить
Но так как были повторяющиеся буквы, мы могли одну и ту же букву посчитать несколько раз, то нам необходимо посчитать количество перестановок всех повторяющихся букв, и поделить на их количество. так как считали мы их зря.
Для буквы И: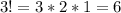
Для буквы Т:
Делим на их произведение, получаем
(x²-6x-9)²-x(x²-4x-9)=0
(x²-6x)²-2(x²-6x)·9+9²-x³+4x²+9x=0
x⁴-12x³+36x²-18x²+108x+81-x³+4x²+9x=0
x⁴-13x³+22x²+117x+81=0
подставив вместо х=-1 убеждаемся, что 1+13+22-117+81=0 - верно
Значит х=-1 - корень данного уравнения
Делим x⁴-13x³+22x²+117x+81 на (х+1)
получим х³-14х²+36х+81
Итак,
x⁴-13x³+22x²+117x+81=(х+1)·(х³-14х²+36х+81)
корни многочлена
х³-14х²+36х+81
следует искать среди делителей свободного коэффициента 81
Это числа ±1;±3;±9
Подставим х=9 и убеждаемся, что 9³-14·9²+36·9+81=81(9-14+4+1)=81·0=0
х=9 - корень данного уравнения
х³-14х²+36х+81 делим на (х-9)
получим х²-5х-9
Осталось разложить на множители последнее выражение
х²-5х-9=0
D=25+36=61
x=(5-√61)/2 или х=(5+√61)/2
Окончательно
x⁴-13x³+22x²+117x+81=0 ⇒(х+1)·(х³-14х²+36х+81)=0⇒(х+1)(х-9)(х²-5х-9)=0⇒ х₁=-1 или х₂=9 или x₃=(5-√61)/2 или х₄=(5+√61)/2