15 , , логорифмическое неравенство. нашла, что x=2 и 64, дальше хз

Показать ответ

Ответ:

Retro2122

11.10.2020 04:12

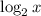$\log_{2}x + 2\sqrt{\log_{2}x} + 8 \geqslant \dfrac{18 - 10\sqrt{\log_{2}x} + 14\log_{2}x}{\log_{2}x - 2\sqrt{\log_{2}x} + 3}$

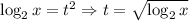
Заметим повторяющееся значения $\log_{2}x$ . Заменим его на новую переменную так, чтобы не было арифметических квадратных корней: $\log_{2}x = t^{2} \Rightarrow t = \sqrt{\log_{2}x}$

Имеем:

$t^{2} + 2t + 8 \geqslant \dfrac{18 - 10t + 14t^{2}}{t^{2} - 2t + 3}$

$\dfrac{14t^{2} - 10t + 18}{t^{2} - 2t + 3} -(t^{2} + 2t + 8) \leqslant 0$

$\dfrac{14t^{2} - 10t + 18 - (t^{2} + 2t + 8)(t^{2} - 2t + 3)}{t^{2} - 2t + 3} \leqslant 0$

$\dfrac{14t^{2} - 10t + 18 - (t^{4} - 2t^{3} + 3t^{2} + 2t^{3} - 4t^{2} + 6t + 8t^{2} - 16t + 24)}{t^{2} - 2t + 3} \leqslant 0$

$\dfrac{14t^{2} - 10t + 18 - t^{4} - 7t^{2} + 10t - 24}{t^{2} - 2t + 3} \leqslant 0$

$\dfrac{-t^{4} + 7t^{2} - 6}{t^{2} - 2t + 3} \leqslant 0$

$\dfrac{t^{4} - 7t^{2} + 6}{t^{2} - 2t + 3}\geqslant 0$

Решим неравенство методом интервалов:

1) ОДЗ:

$t^{2} - 2t + 3 \neq 0$

$D = (-2)^{2} - 4 \cdot 1 \cdot 3 < 0$

$t \in R$

2) Нуль числителя:

$t^{4} - 7t^{2} + 6 = 0$

$t_{1}^{2} = 1; \ \ \ \ t_{2}^{2} = 6$

$t_{1} = \pm 1; \ \ t_{2} = \pm \sqrt{6}$

3) Изобразим координатную прямую и отметим на ней все нули числителя, и определим знак на каждом участке. Те участки, которые будут положительными, и будут решением данного неравенства относительно переменной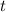 (см. вложение).

Итог: $t \in (-\infty; - \sqrt{6}] \cup [-1; \ 1] \cup [\sqrt{6}; +\infty)$

Это можно записать так:

$\left[\begin{array}{ccc}t \leqslant -\sqrt{6} \ \\\ -1 \leqslant t \leqslant 1\\t \geqslant \sqrt{6} \ \ \ \end{array}\right$

Сделаем обратную замену:

$\left[\begin{array}{ccc}\sqrt{\log_{2}x} \leqslant -\sqrt{6} \ \\\ -1 \leqslant \sqrt{\log_{2}x} \leqslant 1\\\ \sqrt{\log_{2}x} \geqslant \sqrt{6} \ \ \ \end{array}\right$