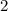16.6. Функцияның анықталу облысын табыңдар: 1) y = arcsin 1/х
2) y = arcsin1/х-2
3) y = 2arccos2/х+2
4) у = 2 - arccos1/х-1
найдите область определения функций​

g - среднегодовое увеличение (умножение) рассчитывается на каждый год (как если бы в каждом году умножение было бы одно и то же)

всего два года, значит за 2 года двухгодовое умножение g*g = 1.17

(за три года было бы g*g*g и т.д.)

g=√1.17=1,0816...

прирост g-1=0,0816... или  8,16%

8,16% это среднегодовой прирост, т.е. если бы в эти 2 года за каждый год прирост был бы один и тот же (эти 8,16%), то окончательный итог был бы таким, как в случае, если в первый год было падение на 10%, а во второй год рост на 30%

Итак, найдем производную от нашей функции :

,

Тогда посчитаем значение производной в точке :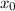

Чтобы найти наибольшее и наименьшее значение функции на отрезке необходимо найти точки экстремума функции (в этих точках функция меняет монотонность) , приравняв производную функции к 0, а затем найти значения функции на концах отрезка и в экстремумах :

1. Находим точки экстремума :

,

,

2. Находим значения функции в точках экстремума и на концах отрезка :

⇒ ,

⇒

⇒

Отсюда делаем вывод, что наибольшее значение функции равно 19, оно достигается в точке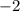 , наименьшее значение равно -13, и оно достигается в точке