164. В одной системе координат построить графики функций: 1) у = 2х и =-2x;
2) g = 3x
хи у=-
— — 3/х;
3) y =-x” и у = -3х2; 4) y=-х и у-х;
5) у = х2 и у = (х – 1); 6) у = х и y = (х + 1)3;
7) y = /х и у = 3х – 2; 8) y=x и у= (х – 3;
9) у = х и y = x3 – 2; 10) y=x и y=x2 + 2.
165. Найти область определения функции:

1)

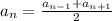
по формуле у нас все совпдает просто подставляем значения

x=0

2) формула n-го члена для последовательности первых членов 3,5,7,9

   формула для n-члена выглядит так:

   a1 это первый член

   n это номер какого то члена (например 17-ый ; 20-ый)

   d это разность то есть на какое число отличается какойто член от предыдущего

   у нас известен первый член и несколько последующих

   нам нужно только найти d вычтем от друг друга два последовательных члена к примеру 7 и 9 получается 2

значит d=2

   Объяснение:

Неравенство верно

Объяснение:

у²-11 = -4·(y²-3·y+11/4) =

= -4·((y²-3·y+9/4)+11/4-9/4) = -4·( (y-3/2)²+1/2)≤ -2 < 0, так как

4·( (y-3/2)²+1/2) = 4·(y-3/2)²+2 ≥ 2

Функция f(y)=12·y-4·у²-11  - эта парабола, a= -4, b= 12, c= -11.

d=b²-4·a·c = 12² - 4·(-4)·(-11) = 144 - 176 <0, это означает, что график параболы не пересекает ось Оу, т.е. график находится целиком выше чем Оу или целиком ниже чем Оу. Коэффициент -4 < 0 при у², так что ветви параболы направлены вниз. Отсюда заключаем, что парабола находится целиком ниже чем Оу, т.е. f(y) < 0