1дана система уравнений: {3a+b=12a−b=0 вычисли значение переменной b. b= 2 дана система двух линейных уравнений: {y+16x=23y−16x=4 найди значение переменной y . ответ: y= 3 реши систему уравнений: {2x−y=20x−5,5y=12 {x= y= 4 реши систему уравнений сложения. {z−3b=52z−4b=36 ответ: z= ; b= 5 реши систему уравнений сложения. ⎧⎩⎨v+13a−4=125a+v3a+11=1 ответ: a= ; v= .
Объяснение:
Так как функции
периодичные с периодом в 
, то значения функции будут повторятся каждые
Далее без ограничений общности, можно утверждать, что от
до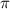 
по осям х и у функция будет иметь график, в то время как для других значений из промежутка для ![x,y\in[-\pi;\pi]](/tpl/images/1430/8946/c0222.png)
графика не будет.
Тогда при
уравнение выполнено тогда, когда соответственно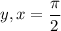 
. Точно также и с 0. Для других значений из-за четности синуса будет 2 значения. Тогда график для ![x,y\in[-\pi;\pi]](/tpl/images/1430/8946/c0222.png)
будет выглядеть "почти" как окружность (Но не окружность). см. рис. 1
Тогда для всех х и у нам необходимо продублировать эту фигуру бесконечное число раз на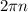
по всем осям . см. рис. 2
РАЗРЫВОВ НИГДЕ НЕТ!
Последняя картинка - график уравнения
В решении.
Объяснение:
y= -2(x+3)² - 4
1. Что является графиком?
График данной функции - парабола со смещённым центром, влево по оси Ох на 3 единицы и вниз по оси Оу на 4 единицы (данные в уравнении).
Поскольку коэффициент при х отрицательный (-2), ветви параболы направлены вниз.
2. Перечислить шаги построения.
а) придать значения х;
б) вычислить значения у;
в) записать полученные данные в таблицу;
г) по точкам построить график.
Дополнительно, для точности построения:
а) определить координаты вершины параболы;
б) найти нули функции (точки пересечения параболой оси Ох, если они существуют).
в) найти точки пересечения параболой оси Оу.
3. Напишите область значений и область определения функции.
Область определения (проекция графика на ось Ох:
D(у): х ∈ R (множество всех действительных чисел), или
D(у): х ∈ (-∞; +∞).
Область значений (проекция графика на ось Оу):
Е(у): [-4; -∞) - в пределах от -4 вниз до - бесконечности.
4. Укажите промежутки возрастания и убывания функции.
Возрастает: (-∞; -4].
Убывает: [-4; -∞).