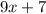2 Чи буде пословесть чеr I, I, II, I appenwoo прогресieio. Якщо a man neplienno 26 Перший член арифметичної прогресії (а) дорівнює 25, а другий 22 Знайдіть ае. 26)
1) к - это угловой коэффициент прямой, он отвечает за то, какой угол образует прямая с положительным направлением оси ОХ, если к>0, то угол острый, если к=0, то прямая параллельна оси ох, если k<0, то угол тупой. по картинкам.
1. k<0; 2. к =0; 3.к>0; 4. к>0
2) b- это ордината точки пересечения прямой с осью ОУ, если b>0 ордината выше оси ох, b<0 ниже, b=0 проходит через начало системы координат. ПО картинкам 1.b>0 ; 2.b>0 ; 3.b=0; 4. b>0
Теперь соединим эти данные в одну картинку.
1k<0;b>0 ;
2к =0;b>0
3.к>0; b=0;
4.к>0b>0
Делаем выводы. 1 - В; 2 D, 3нет таких данных. видимо. опечатка, 4. А, Е. сразу два одинаковых данных. Видимо, здесь тоже опечатка.
1) Для начала разложим многочлен на множители, для этого решим уравнение:
2) Так как данный многочлен делится на с остатком, то представим его в виде
где
- неполное частное;
- искомый остаток.
Степень остатка деления многочлена на многочлен должна быть меньше степени делителя. В данном случае делитель - многочлен второй степени, так что остаток - многочлен первой степени, который имеет вид:
Что необходимо знать?
1) к - это угловой коэффициент прямой, он отвечает за то, какой угол образует прямая с положительным направлением оси ОХ, если к>0, то угол острый, если к=0, то прямая параллельна оси ох, если k<0, то угол тупой. по картинкам.
1. k<0; 2. к =0; 3.к>0; 4. к>0
2) b- это ордината точки пересечения прямой с осью ОУ, если b>0 ордината выше оси ох, b<0 ниже, b=0 проходит через начало системы координат. ПО картинкам 1.b>0 ; 2.b>0 ; 3.b=0; 4. b>0
Теперь соединим эти данные в одну картинку.
1k<0;b>0 ;
2к =0;b>0
3.к>0; b=0;
4.к>0b>0
Делаем выводы. 1 - В; 2 D, 3нет таких данных. видимо. опечатка, 4. А, Е. сразу два одинаковых данных. Видимо, здесь тоже опечатка.
Дано:
Найти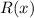
- остаток от деления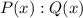 
Решение.
1) Для начала разложим многочлен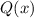
на множители, для этого решим уравнение:
2) Так как данный многочлен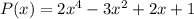
делится на 
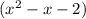с остатком, то представим его в виде
где
Степень остатка деления многочлена на многочлен должна быть меньше степени делителя. В данном случае делитель - многочлен второй степени, так что остаток - многочлен первой степени, который имеет вид:
3) Подставим в равенство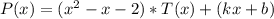
первый корень 
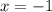и получим:
Вычислим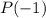
.
Так как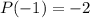
, то
4) Аналогично решаем и со вторым корнем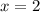
.
5) Подставим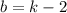
в полученное уравнение:
6)
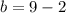
ответ: