Чтобы знаменатель разложить, надо решить квадратное уравнение
Решаем неравенство методом интервалов.
Нули функции
мы уже нашли, когда раскладывали.
Осталось только расположить их на числовой оси и расставить знаки
больше всех, это очевидно. Далее по убыванию , затем , а самое маленькое из них .
Так как дробь была разложена так, что при х во всех скобках коэффициент 1, то в самом правом промежутке "+", а дальше знаки будут чередоватся, так как нет нулей четности кратности (здесь везде степень при скобках равна 1).
Промежутки слева направо будут + - + - +
будут включаться, так как неравенство нестрогое и эти значения с числителя, а со знаменателя значения всегда будут "выколотыми".
Если я правильно понимаю, то неравенство такое
Числитель разложил по формуле разности квадратов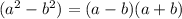
Чтобы знаменатель разложить, надо решить квадратное уравнение
Решаем неравенство методом интервалов.
Нули функции
мы уже нашли, когда раскладывали.
Осталось только расположить их на числовой оси и расставить знаки
Так как дробь была разложена так, что при х во всех скобках коэффициент 1, то в самом правом промежутке "+", а дальше знаки будут чередоватся, так как нет нулей четности кратности (здесь везде степень при скобках равна 1).
Промежутки слева направо будут + - + - +
Это и есть наш ответ
ответ: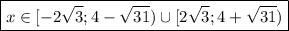
х км/ч (х+1) км/ч
|––––– –––––––|
|––––––––––––––––––|
Дер 32 км Ст
t до ст. = 32/х ч
t до дер. = 32/(х+1) ч
t до ст. – t до дер. = 8/60
32 32 8
–– – –––– = –– домножаем первую дробь на 60(х+1) ОДЗ: 1) х≠0
х х+1 60 вторую дробь на 60х 2) х+1≠0
третью дробь на х(х+1) х≠ –1
32·60(х+1) – 32·60х = 8·х(х+1)
1920х + 1920 – 1920х = 8х² + 8х
8х² + 8х – 1920 = 0 (делим на 8)
х² + х – 240 = 0
D= 1+960=961, √961 =31
х1 = (–1+ 31) : 2 = 30:2 = 15 (км/ч)
х2 = (–1 – 31) : 2 = –32 : 2 = –16 (не имеет смысла)
ответ: Велосипедист ехал до станции со скоростью 15 км/ч.
Задача № 2.
х км/ч (х–4) км/ч
|––––– –––––––|
|––––––––––––––––––|
Гор 16 км Тур
t до тур. = 16/х ч
t до гор. = 16/(х–4) ч
t до тур. + t до гор. = 2ч20мин = 2 цел 20/60 час = 2 цел 1/3 часа = 7/3 часа
16 16 7
–– + –––– = –– домножаем первую дробь на 3(х–4) ОДЗ: 1) х≠0
х х–4 3 вторую дробь на 3х 2) х–4≠0
третью дробь на х(х–4) х≠ 4
16·3(х–4) + 16·3х = 7·х(х–4)
48х – 192 + 48х = 7х² – 28х
7х² – 124х + 192 = 0
D= 124² – 4·7·192 =15 376 – 5 376 = 10 000, √10 000 = 100
х1 = (124 + 100) : 14 = 16 (км/ч) – скорость велосипедиста от города до турбазы
х2 = (124 – 100) : 14 = 12 / 7
16 – 4 = 12 км/ч – скорость от турбазы
ответ: Велосипедист ехал до города со скоростью 12 км/ч.