2. Розв'яжи задачу за до рівняння. Туристи другого дня триденного походу пройшли відстань, утричі більшу, ніж першого дня. Третього дня вони пройшли на 7 км більше, ніж першого дня. Скільки кілометрів пройшли туристи першого дня, Якщо другого дня вони пройшли стільки ж, скільки першого та третьо- го дня разом?
1)
ОДЗ: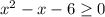 ⇒
⇒ 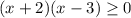 ⇒
⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
два корня или
или 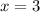
C учетом![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png) получаем ответ:
получаем ответ:
2)
ОДЗ: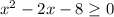 ⇒
⇒ 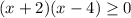 ⇒
⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
два корня или
или 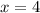
C учетом![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png) получаем ответ:
получаем ответ:
3)
Так как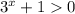 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
D=16-12=4
Показательная функция с основанием 3 возрастает
О т в е т. (0;1)
4)
Так как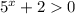 при любых х, возводим данное неравенство в квадрат:
при любых х, возводим данное неравенство в квадрат:
D=36-20=16
Показательная функция с основанием 5 возрастает
О т в е т. (0;1)
Подготовка к ЕГЭ
Задать во Войти
АнонимМатематика23 марта 22:16
найдите сумму корней квадратного уравнения х^2-6x+2=0
ответ или решение1
Михайлов Вячеслав
1. Вспомним формулу дискриминанта:
Дискриминант D квадратного трёхчлена a * x2 + b * x + c равен b2 - 4 * a* c.
Корни квадратного уравнения зависят от знака дискриминанта (D):
D > 0 - уравнение имеет 2 различных вещественных корня (х1 = (-b +√D) / (2 * а)), х2 = (-b -√D) / (2 * а));
D = 0 - уравнение имеет 1 корень (х = (-b +√D) / (2 * а));
D < 0 - уравнение не имеет вещественных корней.
2. Найдём дискриминант заданного уравнения:
D = 36 - 4 * 1 *2;
D = 36 - 8;
D = 28.
3. Дискриминант больше 0, значит уравнение имеет два корня:
х1 = (6 +√28) / (2 * 1);
х1 = (6 + 2√7) / 2;
х1 = 3 + √7;
х2 = (6 - √28) / (2 * 1);
х2 = (6 - 2√7) / 2;
х2 = 3 - √7;
4. Найдём сумму корней уравнения:
х1 + х2 = 3 +√7 + 3 -√7 = 6.
ответ: Сумма корней квадратного уравнения равна 6.бъяснение: