если х₁ и х₂ корни квадратного уравнения, то по т.Виета:
{ х₁ * х₂ = -2/3
{ х₁ + х₂ = 4/3
найдем коэффициенты нового квадратного уравнения...
{
x² + 4x - 6 = 0
и можно сделать проверку:
корни получившегося уравнения D=16+24=40
х₁ = (-4-√40)/2 = -2-√10
х₂ = -2+√10
найдем корни для первого уравнения: D=16+24=40
х₁ = (4-√40)/6 = (2-√10)/3
х₂ = (2+√10)/3
-2-√10 = 2/х₁ = 2 : ((2-√10)/3) = 2*3/(2-√10) = 6*(2+√10)/(-6) = -(2+√10) верно
-2+√10 = 2/х₂ = 2 : ((2+√10)/3) = 2*3/(2+√10) = 6*(2-√10)/(-6) = -(2-√10) верно
если х₁ и х₂ корни квадратного уравнения, то по т.Виета:
{ х₁ * х₂ = -2/3
{ х₁ + х₂ = 4/3
найдем коэффициенты нового квадратного уравнения...
{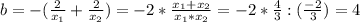
{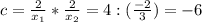
x² + 4x - 6 = 0
и можно сделать проверку:
корни получившегося уравнения D=16+24=40
х₁ = (-4-√40)/2 = -2-√10
х₂ = -2+√10
найдем корни для первого уравнения: D=16+24=40
х₁ = (4-√40)/6 = (2-√10)/3
х₂ = (2+√10)/3
-2-√10 = 2/х₁ = 2 : ((2-√10)/3) = 2*3/(2-√10) = 6*(2+√10)/(-6) = -(2+√10) верно
-2+√10 = 2/х₂ = 2 : ((2+√10)/3) = 2*3/(2+√10) = 6*(2-√10)/(-6) = -(2-√10) верно
5 - √7 7+√ 5 √7 +√5
= 36(5 + √7) + 88(7-√ 5) - 4(√7- √5) =
(5 - √7) (5+ √7) (7+√ 5)(7-√ 5) (√7 +√5)(√7- √5)
= 36(5 + √7) + 88(7-√ 5) - 4(√7- √5) =
5² - √7² 7² -√ 5² √7² - √5²
= 36(5 + √7) + 88(7-√ 5) - 4(√7- √5) =
25 - 7 49 - 5 7 - 5
= 36(5 + √7) + 88(7-√ 5) - 4(√7- √5) =
18 44 2
= 2(5 + √7) + 2(7-√ 5) - 2 (√7- √5) =
1 1 1
= 2(5 + √7) + 2(7-√ 5) - 2 (√7- √5) =
= 10 + 2√7 + 14 - 2√ 5 - 2√7 + 2√5 = 10 + 14 = 24