Диаметр круга - это хорда, которая соединяет две точки его окружности так, что проходит через центр круга.
Дерево 1 - это точка на окружности круга, а дерево 2 - центр окружности. Если диаметр круга = 200м, а длина верёвки чуть больше 200м, то, натянув верёвку с одного берега на другой (можно обойти озеро кругом и прицепить верёвку с другого конца), человек может перебраться по ней, например, перемещая руки одну за другой. Он, конечно, вымокнет, но цель будет достигнута. Если хочется этого избежать, можно закрепить верёвку повыше, чтобы добраться на вису.
Факт в том, что верёвка длиннее диаметра озера и её можно натянуть с одного конца озера на другой, чтобы она как раз через центр озера - дерева 2.
Проще использовать такой подход (он, конечно, на формуле основан)
1. "Разрезать" функцию на 2 части: одну, которую будем дифференцировать, а другую - интегрировать. Понятно, что это разбиение часто основывается на том, какую функцию проще интегрировать, так как продифференцировать можно любую (но иногда, как во 2-м примере, будем смотреть, какую функцию лучше дифференцировать).
2. В столбик написать обе получившиеся функции (ту, которую интегрируем, с дифференциалом запишем, естественно). Отчертить большой чертой и справа напротив каждой функции написать результат того, что мы с ней делаем (в одном случае результат интегрирования, а в другом дифференцирования).
3. А дальше итоговый интеграл будет равен "функция на функцию" (это будет крест накрест, где нет дифференциалов) минус интеграл от произведения функций справа.
Попробую на примере показать:
а) есть интеграл
Здесь удобнее интегрировать логарифм, а дифференцировать
Ну вот как-то так. И теперь сам интеграл:
Надеюсь, что стало понятнее.
б) здесь придется интеграл по частям брать аж 2 раза, но ничего страшного, возьмем.
Сам интеграл
Здесь понятно, что тригонометрия будет давать тригонометрию что при интегрировании, что при дифференцировании, а вот многочлен уже при втором дифференцировании даст константу, так что его и будем дифференцировать.
Надо лишь решить ещё один интеграл, причем абсолютно так же.
Диаметр круга - это хорда, которая соединяет две точки его окружности так, что проходит через центр круга.
Дерево 1 - это точка на окружности круга, а дерево 2 - центр окружности. Если диаметр круга = 200м, а длина верёвки чуть больше 200м, то, натянув верёвку с одного берега на другой (можно обойти озеро кругом и прицепить верёвку с другого конца), человек может перебраться по ней, например, перемещая руки одну за другой. Он, конечно, вымокнет, но цель будет достигнута. Если хочется этого избежать, можно закрепить верёвку повыше, чтобы добраться на вису.
Факт в том, что верёвка длиннее диаметра озера и её можно натянуть с одного конца озера на другой, чтобы она как раз через центр озера - дерева 2.
Есть формула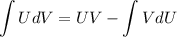
Но напрямую я её использовать не очень люблю.
Проще использовать такой подход (он, конечно, на формуле основан)
1. "Разрезать" функцию на 2 части: одну, которую будем дифференцировать, а другую - интегрировать. Понятно, что это разбиение часто основывается на том, какую функцию проще интегрировать, так как продифференцировать можно любую (но иногда, как во 2-м примере, будем смотреть, какую функцию лучше дифференцировать).
2. В столбик написать обе получившиеся функции (ту, которую интегрируем, с дифференциалом запишем, естественно). Отчертить большой чертой и справа напротив каждой функции написать результат того, что мы с ней делаем (в одном случае результат интегрирования, а в другом дифференцирования).
3. А дальше итоговый интеграл будет равен "функция на функцию" (это будет крест накрест, где нет дифференциалов) минус интеграл от произведения функций справа.
Попробую на примере показать:
а) есть интеграл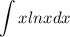
Здесь удобнее интегрировать логарифм, а дифференцировать
Ну вот как-то так. И теперь сам интеграл:
Надеюсь, что стало понятнее.
б) здесь придется интеграл по частям брать аж 2 раза, но ничего страшного, возьмем.
Сам интеграл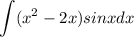
Здесь понятно, что тригонометрия будет давать тригонометрию что при интегрировании, что при дифференцировании, а вот многочлен уже при втором дифференцировании даст константу, так что его и будем дифференцировать.
Надо лишь решить ещё один интеграл, причем абсолютно так же.
Ну и соберем все теперь: