2) за 3 ч диасения по течению реки и 3 ч движения по озеру ка- тер км, а за 4 ч движения против течения реки он на 10 км больше, чем за 3 ч движения по озеру. Най- дите скорость катера и стоячей воде и скорость течения реки.
a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42
Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21
По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6
б) Всего всевозможных исходов: из них нужно взять 2 синих и 1 красный карандаш, таких у нас . Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21
Сиби́рская я́зва (карбункул злокачественный, антракс) — особо опасная инфекционная болезнь сельскохозяйственных и диких животных всех видов, а также человека. Болезнь протекает молниеносно, сверхостро, остро и подостро (у овец и крупного рогатого скота), остро, подостро и ангинозно (у свиней), преимущественно в карбункулёзной форме — у человека. Встречаются также орофарингеальная и гастроинтестинальная формы[1]. Характеризуется интоксикацией, развитием серозно-геморрагического воспалениякожи, лимфатических узлов и внутренних органов; протекает в кожной или септической форме (также у животных встречаются кишечная и лёгочная формы).
a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42
Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21
По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6
б) Всего всевозможных исходов: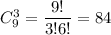 из них нужно взять 2 синих и 1 красный карандаш, таких у нас
из них нужно взять 2 синих и 1 красный карандаш, таких у нас 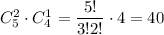 . Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
. Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21