Пусть функция чётна. По определению это значит, что . Получим:
Это значит, что функция тоже чётна.
Теперь пусть функция нечётна. По определению это значит, что . Получим:
Это значит, что функция не является ни чётной, ни нечётной (за исключением случая, когда функция g(x) является нулевой константой).
ответ: если g(x) чётна, то h(x) тоже чётна. Если g(x) нечётна, то h(x) не является ни чётной, ни нечётной (за исключением случая, когда g(x) является нулевой константой, — тогда h(x) является чётной).
Пусть функция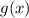
чётна. По определению это значит, что 
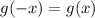. Получим:
Это значит, что функция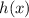
тоже чётна.
Теперь пусть функция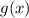
нечётна. По определению это значит, что 
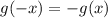. Получим:
Это значит, что функция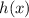
не является ни чётной, ни нечётной (за исключением случая, когда функция g(x) является нулевой константой).
ответ: если g(x) чётна, то h(x) тоже чётна. Если g(x) нечётна, то h(x) не является ни чётной, ни нечётной (за исключением случая, когда g(x) является нулевой константой, — тогда h(x) является чётной).
Итак, пусть у нас есть два натуральных числа. Обозначим их x и y. Пусть y это меньшее из них, тогда по условию x - y = 7;
X*y = 18
Составим систему линейных уравнений с двумя переменными:
{x - y = 7
{x*y = 18
Решим Ее методом подстановки. Выразим из первого выражения y:
{y = x - 7
{xy = 18
Подставим в первое выражение вместо х то что у нас получилось во 2 выражении. И найдём y
{y = x - 7
{x(x-7)=18
{y = x - 7
{x^2 - 7x = 18 => x^2 - 7x - 18 = 0; ( решим по теореме виета ) x1 = 9; -2. Корень -2 не является натуральным числом, значит не удовлетворяет условию задачи
y = 9 - 7 = 2
решением является пара чисел (9 ; 2). Но это в сестеме, а в самой задаче просто 2; 9
ответ : 2;9.