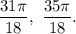Пользуясь тригонометрическими формулами перехода от суммы к произведению, мы получим
Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю.
Корни, удовлетворяющие интервалу :
ответ:
Пользуясь тригонометрическими формулами перехода от суммы к произведению, мы получим
Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю.
Корни, удовлетворяющие интервалу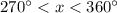 :
:
ответ: