20 вычислить √180/√5 вынести множитель из-под знака корня √48внести множитель под знак корня 5√2сравнить числа √37 и 6зная, что n < 0, внести множитель под знак корня n√7извлечь корень: $\sqrt{(\sqrt{5} - 3)^{2} }$ можно только ответы,

Показать ответ

Ответ:

Olya10783

24.05.2022 23:15

См. рисунок

1. Правильный шестиугольник, состоит из шести равносторонних треугольников.

Найдем сторону шестиугольника AB=r=48/6=8м.

Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD

По теореме Пифагора найдем СD

r²=CD²+DO²=2CD² ⇒ r=CD√2⇒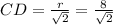 $CD=\frac{r}{\sqrt{2} }= \frac{8}{\sqrt{2}}$ м

$a=2*\frac{8}{\sqrt{2}}=8\sqrt{2}$ м

2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.

Площадь правильного шестиугольника равна

$S=\frac{3\sqrt{3}r^{2}}{2}$ ⇒

$r=\sqrt{\frac{2S}{3\sqrt{3}}}=\sqrt{\frac{2*72\sqrt{3}}{3\sqrt{3}}}=\sqrt{48}=4 \sqrt{3}$ см

Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см

3. Площадь сектора равна

$S=\pi r^{2} *\frac{n}{360}= \pi 12^{2} \frac{120}{360} =\pi \frac{144}{3}$ ≈151 см²

(где n - градусная мера дуги сектора)

1) периметр правильного шестиугольника вписанного в окружность,равен 48м. найди сторону квадрата,впи

0,0(0 оценок)

Ответ:

МАРИШКАНИК

22.09.2020 22:35

Если ПРОЦЕНТНОЕ содеожание МЕДИ в первом сплаве на 15% больше, чем во втором сплаве, то, соответственно, ПРОЦЕНТНОЕ содержание ОЛОВА в первом сплаве будет на 15% меньше, чем во втором сплаве.
Обозначим количество олова в первом сплаве через Х, тогда количество олова во втором сплаве будет равно 1,15 Х.
Составим общее уравнение суммы всех слагаемых сплавов: (6+Х) +(3,6+1,15Х) =60кг.
Решаем его: Х (1+1,15)=60-6-3,6; Х=50,4 / 2,15=23,44кг (олова в первом сплаве)
Во втором сплаве количество олова больше на 15%, то есть равно 1,15Х=1,15*23,44=26,96кг
Всё составляющие сплавов найдены.
Находим массу первого сплава: медь+олово=6+23,44=29,44кг.
Находим массу второго сплава: медь+олово=3,6+26,96=30,56кг

0,0(0 оценок)

Популярные вопросы: Алгебра