25 m/s tezlik bilan yuqoriga tik otilgan jismnimg 2 s dan keyingi tezligi qancha bõladi shu vaqt ichida qancha balandlikka kõtariladi ushbu va keyingi masalalarida g = 10 m/s2 deb olinsin
1) 3sinx-√3 cosx=3; Уравнения вида asinx+bcosx=c решаются следующим образом: 1) нужно разделить обе части уравнения на выражение √(a²+b²); a=3, b=-√3; √(3²+(-√3)²)=√(9+3)=√12=2√3; 2) получаем уравнение вида √3/2sinx-1/2cosx=√3/2; (√3/2=cosπ/6, 1/2=sinπ/6); Далее используем формулу сложения (сумму или разность для синуса): sinx*cosπ/6-cosx*sinπ/6=√3/2; sin(x-π/6)=√3/2; x-π/6=(-1)^(k)*arcsin(√3/2)+πk, k∈Z; x-π/6=(-1)^(k)*π/3+πk,k∈Z; x=(-1)^(k)*π/3+π/6+πk, k∈Z. ответ: (-1)^(k)*π/3+π/6+πk, k∈Z.
Во втором уравнении несколько сложней, так как получаются не табличные значения. Для уравнения вида asinx+bcosx=c есть равносильное уравнение sin(x+α)=c/√(a²+b²), где α=arccos a/√(a²+b²), α=arcsin b/√(a²+b²), α=arctg b/a. 2) 4sinx+6cosx=1; a=4, b=6, √(4²+6²)=√(16+36)=√52=2√13; В этом уравнении удобнее взять α=arctg b/a=arctg 6/4=arctg 3/2. Получаем sin(x+arctg 3/2)=√13/26; x=(-1)^(k)*arcsin √13/26-arctg 3/2+πk, k∈Z. ответ: (-1)^(k)*arcsin √13/26-arctg 3/2+πk, k∈Z.
ответ: 65 км/ч
Объяснение:
1) 312 : 2 = 156 (км) - половина расстояния
2) 12 мин = 12/60 ч = 1/5 ч
Скорость Время Расстояние
До остановки x - 5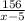 156
156
После ост. x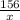 156
156
Время до остановки на 12 мин больше времени после остановки:
х > 5 по смыслу задачи, поэтому умножим обе части уравнения на
5x(x - 5):
780x - 780(x - 5) = x(x - 5)
780x - 780x + 3900 = x² - 5x
x² - 5x - 3900 = 0
По теореме Виета:
x₁ · x₂ = - 3900
x₁ + x₂ = 5
Значит, x₁ = - 60 - не подходит по смыслу задачи
x₂ = 65
ответ: 65 км/ч
Уравнения вида asinx+bcosx=c решаются следующим образом:
1) нужно разделить обе части уравнения на выражение √(a²+b²);
a=3, b=-√3; √(3²+(-√3)²)=√(9+3)=√12=2√3;
2) получаем уравнение вида
√3/2sinx-1/2cosx=√3/2; (√3/2=cosπ/6, 1/2=sinπ/6);
Далее используем формулу сложения (сумму или разность для синуса):
sinx*cosπ/6-cosx*sinπ/6=√3/2;
sin(x-π/6)=√3/2;
x-π/6=(-1)^(k)*arcsin(√3/2)+πk, k∈Z;
x-π/6=(-1)^(k)*π/3+πk,k∈Z;
x=(-1)^(k)*π/3+π/6+πk, k∈Z.
ответ: (-1)^(k)*π/3+π/6+πk, k∈Z.
Во втором уравнении несколько сложней, так как получаются не табличные значения.
Для уравнения вида asinx+bcosx=c есть равносильное уравнение
sin(x+α)=c/√(a²+b²), где α=arccos a/√(a²+b²), α=arcsin b/√(a²+b²), α=arctg b/a.
2) 4sinx+6cosx=1;
a=4, b=6, √(4²+6²)=√(16+36)=√52=2√13;
В этом уравнении удобнее взять α=arctg b/a=arctg 6/4=arctg 3/2.
Получаем
sin(x+arctg 3/2)=√13/26;
x=(-1)^(k)*arcsin √13/26-arctg 3/2+πk, k∈Z.
ответ: (-1)^(k)*arcsin √13/26-arctg 3/2+πk, k∈Z.