ответ:a>0: ; a=0:x=0
Объяснение:
и ограничения на a:
a>0
Если же a=0:
Решение имеет только второе уравнение => x=0
ответ:a>0: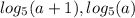 ; a=0:x=0
; a=0:x=0
Объяснение:
и ограничения на a:
a>0
Если же a=0: