Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Для ∈
Для ∈
Решаем систему:
Четыре уравнения.
1) ⇒
Выполняется для любых .
2) ⇒ ⇒
Дробь может быть меньше либо равно нулю тогда и только тогда, когда ее числитель неотрицателен, а знаменатель отрицателен, либо когда ее числитель отрицателен или равен нулю, а знаменатель положителен, т.е. в первом случае:
∈∅ (ни один не удовлетворяет данному условию, так как всегда положителен)
Решая уравнение sin²(x)-3*sin(x)+2=0, находим sin(x)=1 либо sin(x)=2. Но так как /sin(x)/≤1, то равенство sin(x)=2 невозможно. Запишем теперь данное неравенство в виде 3*[sin(x)-1]*[sin(x)-2]≥0. Так как sin(x)-2<0 при любом значении x, то неравенство 3*[sin(x)-1]*[sin(x)-2]>0 возможно только при sin(x)-1<0, т.е. при sin(x)<1. А это неравенство верно при любых значениях x, кроме значений x=π/2+2*π*n, где n∈Z. Но так как значение sin(x)=1 тоже удовлетворяет исходному неравенству, то отсюда следует, что оно справедливо при любых значениях x, т.е. при x∈(-∞;∞).
ответ: ∈
∈ ![[-5 ; -\sqrt{3}]](/tpl/images/1008/3859/da582.png) ∪
∪ ![[\sqrt{3};5]](/tpl/images/1008/3859/34029.png)
Объяснение:
Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Для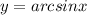
 ∈
∈![[-1 ; 1]](/tpl/images/1008/3859/dff6b.png)
Для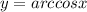
 ∈
∈![[-1 ; 1]](/tpl/images/1008/3859/dff6b.png)
Решаем систему:
Четыре уравнения.
1)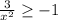 ⇒
⇒ 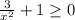
Выполняется для любых .
.
2)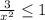 ⇒
⇒ 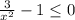 ⇒
⇒
Дробь может быть меньше либо равно нулю тогда и только тогда, когда ее числитель неотрицателен, а знаменатель отрицателен, либо когда ее числитель отрицателен или равен нулю, а знаменатель положителен, т.е. в первом случае:
Во втором случае:
3)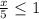 ⇒
⇒ 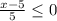 ⇒
⇒ 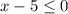 ⇒
⇒ 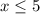
4) Аналогично третьему уравнению находим:
Находим пересечение всех полученных промежутков:
1) ∀
2) ∈
∈ ![(-\infty;-\sqrt{3}]](/tpl/images/1008/3859/aebdf.png) ∪
∪ 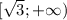
3)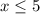
4)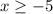
ответ: ∈
∈ ![[-5 ; -\sqrt{3}]](/tpl/images/1008/3859/da582.png) ∪
∪ ![[\sqrt{3};5]](/tpl/images/1008/3859/34029.png)
ответ: x∈(-∞;∞).
Объяснение:
Решая уравнение sin²(x)-3*sin(x)+2=0, находим sin(x)=1 либо sin(x)=2. Но так как /sin(x)/≤1, то равенство sin(x)=2 невозможно. Запишем теперь данное неравенство в виде 3*[sin(x)-1]*[sin(x)-2]≥0. Так как sin(x)-2<0 при любом значении x, то неравенство 3*[sin(x)-1]*[sin(x)-2]>0 возможно только при sin(x)-1<0, т.е. при sin(x)<1. А это неравенство верно при любых значениях x, кроме значений x=π/2+2*π*n, где n∈Z. Но так как значение sin(x)=1 тоже удовлетворяет исходному неравенству, то отсюда следует, что оно справедливо при любых значениях x, т.е. при x∈(-∞;∞).