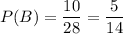2arcsin(-√3:2)+arctg (-1)+arccos ✓2:2
​

y=kx+1 и y=kx^2−(k−3)x+k приравниваем, решаем и требуем чтобы было 2 корня D>0

kx+1=kx^2−(k−3)x+k

kx^2-(k-3)x+k-kx-1=0

kx^2-(2k-3)x+k-1=0

D=(2k-3)^2-4k(k-1)=4k^2-12k+9-4k^2+4k=-8k+9>0

8k<9

k<9/8

теперь y=kx+1 и y=(2k−1)x^2−2kx+k+9/4 приравниваем и требуем чтобы не было корней D<0

kx+1=(2k−1)x^2−2kx+k+9/4

(2k−1)x^2−2kx+k+9/4-kx-1=0

(2k−1)x^2−3kx+k+5/4=0

D=(3k)^2-4(2k-1)(k+5/4)=9k^2-(2k-1)(4k+5)=9k^2-8k^2+4k-10k+5=k^2-6k+5=(k-1)(k-5)<0

1<k<5

пересекаем k<9/8 и 1<k<5 - ответ 1<k<9/8

ответ 1<k<9/8

ответ: 1) 9/28; 2) 5/14.

Пошаговое объяснение:

1) А — сумма цифр на кости домино менее 4;

Общее число возможных исходов элементарных исходов равно числу которыми можно взять одну кость домино из 28

Число исходов, благоприятствующих событию А: нужно найти количество всех костей домино, в которой сумма цифр взятой кости домино менее 4.

Т.е. число исходов, благоприятствующих событию А, равно 9.

— вероятность того, что сумма цифр на ней менее 4.

2) Общее число возможных исходов элементарных исходов равно 28(с пункта 1).

B — обе цифры на ней четные.

Число исходов, благоприятствующих событию В равно числу достать одну кость домино с четными цифрами.

Всего таких костей домино: 10 (из перечень костей домино на картинке легко увидеть)

Вероятность события В: