Точки, равноудалённые от данной прямой (по одну её сторону) , образуют прямую, параллельную данной. Это одна из формулировок пятого постулата Евклида: "Если [на плоскости] при пересечении двух прямых третьей сумма внутренних односторонних углов меньше двух прямых, то эти прямые при достаточном продолжении пересекаются, и притом с той стороны, с которой эта сумма меньше двух прямых. " Пятый постулат чрезвычайно сильно отличается от других постулатов Евклида, простых и интуитивно очевидных (см. Начала Евклида) . Поэтому в течение 2 тысячелетий не прекращались попытки исключить его из списка аксиом и вывести как теорему. Все эти попытки окончились неудачей. «Вероятно, невозможно в науке найти более захватывающую и драматичную историю, чем история пятого постулата Евклида» [3]. Несмотря на отрицательный результат, эти поиски не были напрасны, так как в конечном счёте привели к полному пересмотру научных представлений о геометрии Вселенной.
ответ: 20.4 кг.
Объяснение:
пусть в 1) сосуде (х) кг кислоты; во 2) (у) кг кислоты;
тогда по условию х+у = 0.8*50
(30кг+20кг=50кг; 80% от числа находим, умножая на 80/100)
х+у = 40 ---> y = 40-x
возьмем равные массы растворов (например, по 1 кг)
1)
в 30 кг ---> x кг кислоты
в 1 кг ---> (x/30) кг кислоты
2)
в 20 кг ---> (40-x) кг кислоты
в 1 кг ---> (40-х)/20 кг кислоты
получим второе уравнение: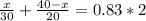
(1кг+1кг=2кг; 83% от числа находим, умножая на 83/100)
умножим обе части равенства на 60 (чтобы вычислять без дробей)
2х + 120 - 3х = 99.6
х = 20.4
и можно проверить:
20.4 + 40 - 20.4 = 8*5 (очевидно)
1) в 1 кг раствора содержится 20.4/30 = 204/300 = 68/100 кг кислоты
2) в 1 кг раствора содержится 19.6/20 = 196/200 = 98/100 кг кислоты
если смешать, получится (68+98)/100 = 166/100
это =2*0.83
Это одна из формулировок пятого постулата Евклида:
"Если [на плоскости] при пересечении двух прямых третьей сумма внутренних односторонних углов меньше двух прямых, то эти прямые при достаточном продолжении пересекаются, и притом с той стороны, с которой эта сумма меньше двух прямых. "
Пятый постулат чрезвычайно сильно отличается от других постулатов Евклида, простых и интуитивно очевидных (см. Начала Евклида) . Поэтому в течение 2 тысячелетий не прекращались попытки исключить его из списка аксиом и вывести как теорему. Все эти попытки окончились неудачей. «Вероятно, невозможно в науке найти более захватывающую и драматичную историю, чем история пятого постулата Евклида» [3]. Несмотря на отрицательный результат, эти поиски не были напрасны, так как в конечном счёте привели к полному пересмотру научных представлений о геометрии Вселенной.