2sin(3pi/2+x)cos(pi/2+x)=корень из 3* cos(2pi-x) найти х в промежутке [-2pi; -pi]

Найдем сумму чисел в первой группе:

Найдем сумму чисел во второй и третьей группе:

Заметим, что во второй и третьей группе вместе чисел было:

Введем обозначения. Пусть во второй группе было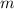 чисел, а в третьей группе было 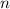чисел. Среднее арифметическое чисел второй группы по условие равно 59, а среднее арифметическое чисел третьей группы обозначим как .

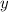В этих обозначениях нам нужно найти .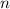

Можем записать два равенства:

Из первого равенства выразим :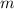

Подставим во второе равенство:

Так как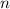 - количество чисел, то это число должно быть целым (как минимум, неотрицательным). Также, по с условию 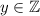. Значит, число 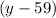является делителем числа . Тогда есть 4 варианта:

Однако, не все эти 4 варианта реализуемы. Вспомним, что количество чисел третьей группы связано с количеством чисел второй группы соотношением:

Так как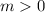 , то:

Такому условию удовлетворяет только вариант .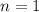

ответ: 1

x = arctg(-0.4)+\pi kx=arctg(−0.4)+πk ; x = \frac{\pi }{4} + \pi nx=

4

π

+πn

Пошаговое объяснение:

5sin^{2}x - 3sinxcosx - 2cos^{2}x = 05sin

2

x−3sinxcosx−2cos

2

x=0

Разделим уравнение на cos^{2}xcos

2

x :

5tg^{2}x - 3tgx - 2 = 05tg

2

x−3tgx−2=0

Проведем замену t = tgx:

5t^{2} - 3t - 2 = 05t

2

−3t−2=0

Решим квадратное уравнение методом коэффициентов:

a + b + c = 0a+b+c=0

5 - 3 - 2 = 05−3−2=0 ⇒ t_{1} = 1t

1

=1 ; t_{2} = c/a = -0.4t

2

=c/a=−0.4

Проведем обратную замену:

tgx = 1tgx=1

x = arctg 1x=arctg1

x = \frac{\pi }{4} + \pi nx=

4

π

+πn , где n ∈ Z

tgx = -0.4tgx=−0.4

x = arctg(-0.4)x=arctg(−0.4)

x = arctg(-0.4)+\pi kx=arctg(−0.4)+πk , где k ∈ Z