Пусть у Егора было х моделей.
По условию он расставил модели самолетов поровну на 14 полках => х = 14 а
потом он переставил их тоже поровну на 8 полок => х = 8 b
где а и b - это натуральные числа, т.к. это количество самолетов на полках.
Итак, 14 а = 8 b
7а = 4 b
Т.о. число х одновременно кратно 7 и 4 и по усл. 100<х<120 = >
х кратно 7 = > х ∈ {... 105; 112; 119...}
х кратно 4 = > х ∈ {... 100; 104; 108; 112; 116...}
Это число 112 = > у Егора всего 112 моделей.
ответ: 112.
Для начала найдем ОДЗ:
Первое уравнение решим отдельно.
3x^2 -2>0
3x^2 -2=0
x^2=2/3
Чертим координатную прямую, отмечаем точки, расставляем знаки. Рисунок добавлю во влажения.
Решением этого уравнения будет промежуток
А решением системы будет являться
Теперь начнем решение. Представим 4 в виде логорифма по основанию x.
Так как основания равны, то знак логорифма можно опустить.
3x^2 -2 =x^4
x^4 - 3x^2 +2 =0
Это биквадратное уравнение. Введем обозначения
x^2 = a,
a^2 -3a+2=0
По теореме Виета a1=2, a2=1
Теперь найдем х:
x^2= 2 x^2=1
x=±1
Выберем корни, входящие в ОДЗ. Таковыми являются и 1.
ответ: и 1
Пусть у Егора было х моделей.
По условию он расставил модели самолетов поровну на 14 полках => х = 14 а
потом он переставил их тоже поровну на 8 полок => х = 8 b
где а и b - это натуральные числа, т.к. это количество самолетов на полках.
Итак, 14 а = 8 b
7а = 4 b
Т.о. число х одновременно кратно 7 и 4 и по усл. 100<х<120 = >
х кратно 7 = > х ∈ {... 105; 112; 119...}
х кратно 4 = > х ∈ {... 100; 104; 108; 112; 116...}
Это число 112 = > у Егора всего 112 моделей.
ответ: 112.
Для начала найдем ОДЗ:
Первое уравнение решим отдельно.
3x^2 -2>0
3x^2 -2=0
x^2=2/3
Чертим координатную прямую, отмечаем точки, расставляем знаки. Рисунок добавлю во влажения.
Решением этого уравнения будет промежуток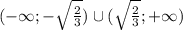
А решением системы будет являться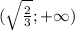
Теперь начнем решение. Представим 4 в виде логорифма по основанию x.
Так как основания равны, то знак логорифма можно опустить.
3x^2 -2 =x^4
x^4 - 3x^2 +2 =0
Это биквадратное уравнение. Введем обозначения
x^2 = a,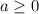
a^2 -3a+2=0
По теореме Виета a1=2, a2=1
Теперь найдем х:
x^2= 2 x^2=1
Выберем корни, входящие в ОДЗ. Таковыми являются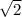 и 1.
и 1.
ответ: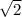 и 1
и 1