4
Объяснение:
Сделаем замену на q
Уравнение тогда примет вида:
D=400-256=144
ОБРАТНАЯ ЗАМЕНА:
ИЛИ
А ТЕПЕРЬ ЗАПИШЕМ НАИБОЛЬШИЙ КОРЕНЬ:
ЭТО 4
Заменим х²=у≥0, получим квадратное уравнение у²-20у+64=0, По Виету у=16, у=4, возвратимся к старой переменной. х²=16, х=±4, х²=4; х=±2, наибольший из корней -4;-2;2;4 последний. т.е. 4
ответ 4
4
Объяснение:
Сделаем замену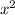 на q
на q
Уравнение тогда примет вида:
D=400-256=144
ОБРАТНАЯ ЗАМЕНА:
ИЛИ
А ТЕПЕРЬ ЗАПИШЕМ НАИБОЛЬШИЙ КОРЕНЬ:
ЭТО 4
Заменим х²=у≥0, получим квадратное уравнение у²-20у+64=0, По Виету у=16, у=4, возвратимся к старой переменной. х²=16, х=±4, х²=4; х=±2, наибольший из корней -4;-2;2;4 последний. т.е. 4
ответ 4