Формула площади трапеции S=mh=(AB+CD/2)h Зная радиус вписанной окружности, мы устанавливаем, что h=2r=6 Далее по т. о касательных, а так же зная, что трапеция равнобокая, мы имеем AC=12, AB=CD=x+6 BC=2x Находим по формуле длину отрезка между высотой из угла при меньшем основании и углом при большем основании: АС-ВС/2 = 6-х Так как высота - перпендикуляр, можно утверждать, что по т. Пифагора: (x-6)^2+h^2=(x+6)^2 т. е. 36+12х+х^2-36+12x-x^2=h^2 => 24x=36 => x=1.5 Далее вычисляем основания и считаем площадь: (12+3/2)*6=45 ответ: S=45 ед^2
Пусть двузначное число составлено из двух цифр a и b, причём a≠0 и b≠0. Тогда число можно представить в виде суммы .
Сразу проверим случай a=b : . Так как число 11 - простое (делители 1 и 11), только число 11 будет кратно 1·1. Другие двузначные числа не подходят под условие.
Число кратно произведению цифр ab.
Так как числа ka и 1 - целые, значит, дробь должна тоже стать целым числом. Знаменатель b должен быть равен 1 или сократиться.
4) Число a или число 2a должны быть кратны цифре b. Возможные пары, помимо рассмотренных : (2;4), (3,6), (4,8), (6,3), (8,4), (9,3)
Далее по т. о касательных, а так же зная, что трапеция равнобокая, мы имеем AC=12, AB=CD=x+6 BC=2x Находим по формуле длину отрезка между высотой из угла при меньшем основании и углом при большем основании: АС-ВС/2 = 6-х Так как высота - перпендикуляр, можно утверждать, что по т. Пифагора: (x-6)^2+h^2=(x+6)^2 т. е. 36+12х+х^2-36+12x-x^2=h^2 => 24x=36 => x=1.5 Далее вычисляем основания и считаем площадь: (12+3/2)*6=45 ответ: S=45 ед^2
Пусть двузначное число составлено из двух цифр a и b, причём a≠0 и b≠0. Тогда число можно представить в виде суммы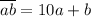 .
.
Сразу проверим случай a=b :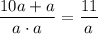 . Так как число 11 - простое (делители 1 и 11), только число 11 будет кратно 1·1. Другие двузначные числа не подходят под условие.
. Так как число 11 - простое (делители 1 и 11), только число 11 будет кратно 1·1. Другие двузначные числа не подходят под условие.
Число кратно произведению цифр ab.
Так как числа ka и 1 - целые, значит, дробь должна тоже стать целым числом. Знаменатель b должен быть равен 1 или сократиться.
4) Число a или число 2a должны быть кратны цифре b. Возможные пары, помимо рассмотренных : (2;4), (3,6), (4,8), (6,3), (8,4), (9,3)
a = 2; b = 4;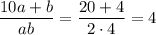
a = 3; b = 6;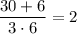
Остальные варианты не подходят
a = 4; b = 8;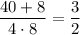 a = 6; b = 3;
a = 6; b = 3; 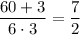
a = 8; b = 4;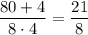 a = 9; b = 3;
a = 9; b = 3; 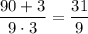
ответ : 11, 12, 15, 24, 36