3. Разложите на множители. а); в);
б); г). (2б.)

4. Упростите выражение (2а – b)2 – (b + 2а)2 .
а) 8аb; в) –b2(2а)2;
б) – 8аb; г) 8а2. (3б.)
5. Найдите значение выражения
(a – 3)2 – 2(a – 3)(a + 3) + (a + 3)2приa = – .
а)–36; в)36;
б)49; г)–49. (3б.)

Показать ответ

Ответ:

димон7777

09.06.2022 03:34

Заметим, что если пара (x₀, y₀) – решение системы, то и пара (x₀, -y₀) также является решением системы. Доказывается это подстановкой -y вместо y в уравнения:

В первом уравнении рассмотрим только первые две скобки:

$(3-2\sqrt{2})^{-y}+(3+2\sqrt{2})^{-y}=\frac{1}{(3-2\sqrt{2})^{y}}+\frac{1}{(3+2\sqrt{2})^{y}}=\frac{(3+2\sqrt{2})^{y}}{(3-2\sqrt{2})^{y}(3+2\sqrt{2})^{y}}+\\+\frac{(3-2\sqrt{2})^{y}}{(3+2\sqrt{2})^{y}(3-2\sqrt{2})^{y}}=\frac{(3+2\sqrt{2})^{y}}{(3^2-(2\sqrt{2})^2)^y}+\frac{(3-2\sqrt{2})^{y}}{(3^2-(2\sqrt{2})^2)^y}=\frac{(3+2\sqrt{2})^{y}}{1^y}+\frac{(3-2\sqrt{2})^{y}}{1^y}=\\=(3+2\sqrt{2})^y+(3-2\sqrt{2})^y$

После замены y на -y сумма не изменилась, значит, уравнение осталось тоже неизменным.

Во втором уравнении при подстановке -y минус «съедается» квадратом, поэтому уравнение также остаётся неизменным.

Исходя из этого единственным решение бывает тогда, когда y = -y, то есть y = 0. Получаем такую систему:

$\begin{equation*}\begin{cases}2-3a=x^2+6x+5,\\(a^2-5a+6)x^2=0,\\-6\leq x\leq 0\end{cases}\end{equation*}$

Рассмотрим функцию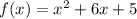 f(x)=x^2+6x+5 на промежутке -6 ≤ x ≤ 0. Вершина этой параболы находится в точке с абсциссой -3, ось симметрии ровно посередине заданного промежутка. Значит, при x = -3 парабола принимает ровно одно значение, а при всех остальных заданных x – ровно два. Отсюда единственность решения достигается:

1) x = -3 (единственное решение первого уравнения), причём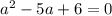 a^2-5a+6=0 , иначе не будет решений второго уравнения;

2) x = 0 (единственное решение второго уравнения).

Случай, когда первое уравнение имеет два решения, а второе – только одно из них, не достигается.

Случай 1 (x = -3):

$2-3a=(-3)^2+6*(-3)+5 \Leftrightarrow 2-3a=-4 \Leftrightarrow a=2$

При таком a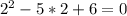 2^2-5*2+6=0 - верно, значение подходит.

Случай 2: (x = 0):

$2-3a=0^2+6*0+5 \Leftrightarrow 2-3a=5 \Leftrightarrow a=-1$ .

Проверка значений параметра на посторонние решения:

При a = 2 из второго уравнения следует, что y = 0, тогда из первого следует, что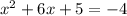 x^2+6x+5=-4 , это уравнение также имеет единственное решение.

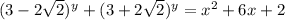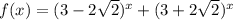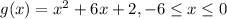При a = -1 первое уравнение имеет вид $(3-2\sqrt{2})^y+(3+2\sqrt{2})^y=x^2+6x+2$ . Рассмотрим функции $f(x)=(3-2\sqrt{2})^x+(3+2\sqrt{2})^x$ и $g(x)=x^2+6x+2, -6\leq x\leq 0$ .

$f'(x)=((3-2\sqrt{2})^x+(3+2\sqrt{2})^x)'=((3-2\sqrt{2})^x)'+((3+2\sqrt{2})^x)'=\\=(3-2\sqrt{2})^x\ln{(3-2\sqrt{2})}+(3+2\sqrt{2})^x\ln{(3+2\sqrt{2})}=\\=(3+2\sqrt{2})^x\ln{(3+2\sqrt{2})}-(3-2\sqrt{2})^x\ln{(3+2\sqrt{2})}=\\=\ln{(3+2\sqrt{2})}((3+2\sqrt{2})^x-(3-2\sqrt{2})^x)$

Нули производной:

$\ln{(3+2\sqrt{2})}((3+2\sqrt{2})^x-(3-2\sqrt{2})^x)=0\\(3+2\sqrt{2})^x=(3-2\sqrt{2})^x\\x=0$

Функция убывает при x ≤ 0 и возрастает при x ≥ 0. Значит, x = 0 – точка глобального минимума. Минимальное значение функции f(0) = 2. Значит, E(f) = [2; +∞).

g(x) – парабола. При заданных ограничениях E(g) = [-4; 2]. Значит, решение первого уравнения существует, если:

$\left \{ {{f(y)=2} \atop {g(x)=2}} \right. \left \{ {{y=0} \atop {x=-6; 0}} \right.$

Вид второго уравнения при a = -1: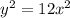 y^2=12x^2 . Пара решений (-6; 0) не является его решением. Пара (0; 0) является его решением. Значит, система имеет единственное решение.

ответ: -1; 2

0,0(0 оценок)

Ответ:

PauD

18.08.2020 23:35

7час50мин-6час 20мин=1час30мин=1,5ч - время в пути до встречи при одновременном выезде
180:1,5=120(км/ч) - скорость сближения
6ч20мин-1ч15мин=5ч 05мин - время выезда автобуса, если бы он выехал раньше на 1ч15мин
6ч20мин+15мин=6ч35мин - время выезда автомобиля, если бы он выехал на 15 мин позже
7ч35мин-5ч05мин=2ч30мин=2,5час - время в пути до встречи автобуса, если бы он выехал раньше на 1ч15мин
7ч35мин-6ч35мин=1час - время в пути автомобиля, если бы он выехал раньше на 1ч15мин

Пусть (х км/ч) - скорость автобуса
у (км/ч) - скорость автомобиля
2,5х (км) - проедет до встречи автомобиль, если выедет раньше
у*1=у(км) - расстояние проедет до встречи автобус, если выедет позже
х+у=120(км/ч) - скорость сближения
Составим систему уравнений:
х+у=120 }
2,5х+у=180 }

х=120-у, подставим значение х во второе уравнение:
2,5(120-у)+у=180
300-2,5у+у=180
1,5у=120
у=120:1,5
у=80(км/ч) - скорость автомобиля
120-80=40(км/ч) - скорость автобуса

0,0(0 оценок)

Популярные вопросы: Алгебра