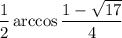30. найти значение выражения (1+17)cos 2x , где хо — наимень-
ший положительный корень уравнения 2sin² x+cos 4x -2 = 0.

Question

Алгебра: 30. найти значение выражения (1+17)cos 2x , где хо — наимень-ший положительный корень уравнения 2sin² x+cos 4x -2 = 0.

bar569 · Answer

Решаем как квадратное уравнение относительно cos2x - уравнение решений не имеет. откуда  Наименьший положительный корень будет при n = 0 равны...