32. Составьте квадратное уравнение по его корням: 1) 2; 7; 4)-2,1; -0,3; 7) 1/2; 3/5;

Обозначим cлагаемые за Х,У,Z

(X+Y+Z)/3>=1

Согласно неравенству о среднем арифметическом и среднем геометрическом достаточно доказать :

ХУZ>=1

Вернемся к исходным обозначениям

8abc>=(a+b)(b+c)(a+c)

Снова согласно неравенству о среднем арифметическом и среднем геометрическом видим

a+b>=2sqrt(ab)   b+c>=2sqrt(сb) (a+c)>=2sqrt(ac)

поэтому можим заменить сомножители справа на произведение

2sqrt(ab)*2sqrt(aс)*2sqrt(сb)=8abc,   что и доказывает неравенство.

Равенство достигается только при а=с=b

Объяснение:

117

1 √64 = 8    (64 = 8²)

2 ∛27 = 3    (27 = 3³)

3. = ∛8² = 4    (8 = 2³)

4.  = ³ = 3³ = 27   (81 = 3⁴)

5.  = 1/³ = 1/8  (16 = 2⁴)

6. =1/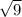 ³ = 1/3³ = 1/27

118    ^ - знак степени  -после него показатель степени

1.  = 2^ (4/5 + 11/5)= 2^15/5 = 2³ = 8, (степень равна сумме степеней и равна 15/5)

2.  = 5^ (2/7 + 5/7) = 5^ 7/7 = 5¹ = 5

3.  = 9^4/6 * 9^1/6 = 9^5/6 = 3^5/3 = ∛27∛9= 3∛9

4.  = 4^2/6 / 4^5/6 =  1/ 4^3/6 = 1/√4 = 1/2

5.  = 7² = 49

6.  = 1/∛8 = 1/2

7. = 8^ 12/15 / 8^ 7/15 = 8^ 5/15 = ∛8 = 2

8.  = 5³ = 125

119

1), = 3^4/5 * 3^6/5 = 3^ 10/5 = 3³ = 9

2) = 7^ 2/3 * 7^ 4/3 = 7² = 49

3) 144 = 12²

= √12³/√3³ = √4³ = 2³ = 8

4) = √(150/6)³ = √25³ = 5³ = 125