5.
Поскольку x и y - натуральные числа,
Следовательно, произведение этих чисел является составным числом.
6. Заметим, что 2020=2019+1. Будем решать задачу в более общем виде. А именно, докажем, что при любом целом a выражение
является квадратом целого числа. Имеем:
5.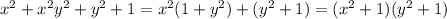
Поскольку x и y - натуральные числа,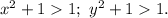
Следовательно, произведение этих чисел является составным числом.
6. Заметим, что 2020=2019+1. Будем решать задачу в более общем виде. А именно, докажем, что при любом целом a выражение