Находи точки экстремума, для этого приравниваем производную к нулю.
Не входит в данный промежуток
Входит в данный промежуток
-3 входит в данный промежуток, надо определить это точка макимума или минимума. Для этого берем любое значение из данного промежутка, например, -2, справа от этой точки, и подставляем его в производную и смотрим знак.
y'(-2) < 0
Значит х = -3 является точкой максимума. Т.е в этом промежутке и в этой точке находится наибольшее значение функции. Подставляем -3 в функцию.
y(-3) =
Находи точки экстремума, для этого приравниваем производную к нулю.
Входит в данный промежуток
Не входит в данный промежуток
-2 входит в данный промежуток, надо определить это точка макимума или минимума. Для этого берем любое значение из данного промежутка, например, 0, справа от этой точки, и подставляем его в производную и смотрим знак.
y(0) < 0
Значит х = -2 является точкой максимума. Т.е в этом промежутке и в этой точке находится наибольшее значение функции. Подставляем -2 в функцию.
пусть 1 блакнот = x,1 тетрадь = y
состовляем систему уравнений:
3x+2y=40, 2y=40-3x, y=(40-3x)/2 , y=(40-3x)/2 , y=(40-3x)/2,
2x+4y=32; 2x+4y=32; 2x+4*(40-3x\2)=32; 2x+80-6x=32; -4x=-48;
y=(40-3x)/2, y=(40-3x)/2 , y=(40-(3*12))/2, y=23,
4x=48 ; x=12; x=12; x=12.
ответ:тетрадь=2р блакнот= 12р
ПРОВЕРКА:
3*12+2*2=36+4+40
2*12+4*2=24+8=32
x ≠ 0
Находи точки экстремума, для этого приравниваем производную к нулю.
-3 входит в данный промежуток, надо определить это точка макимума или минимума. Для этого берем любое значение из данного промежутка, например, -2, справа от этой точки, и подставляем его в производную и смотрим знак.
y'(-2) < 0
Значит х = -3 является точкой максимума. Т.е в этом промежутке и в этой точке находится наибольшее значение функции. Подставляем -3 в функцию.
y(-3) =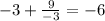
Находи точки экстремума, для этого приравниваем производную к нулю.
-2 входит в данный промежуток, надо определить это точка макимума или минимума. Для этого берем любое значение из данного промежутка, например, 0, справа от этой точки, и подставляем его в производную и смотрим знак.
y(0) < 0
Значит х = -2 является точкой максимума. Т.е в этом промежутке и в этой точке находится наибольшее значение функции. Подставляем -2 в функцию.
y(-2) =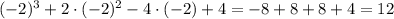
Про второй номер, к сожалению не смогу.