1)
Прибавим к 1му уравнению второе и получим:
2(х+y)=-12
x+y=-6
x=-6-y
Подставим допустим во 2 уравнение системы, получим
-6-y+y-(6+y)y=2
По теореме Виета корни будут:
Находим х, получаем
ответ: решением системы являются пары чисел (х,у): (-4,-2), (-2, -4)
2)
Выразим из второго уравнения х, получим:
, только при условии, что (это рассмотрим отдельно)
Теперь подставляем х=1 в 1 уравнение системы и получаем:
По теореме Виета:
Теперь рассмотрим случай, когда y=1, является ли он решением:
Подставляем в 1 и 2 уравнение системы и получаем:
По теореме Виета получаем
Т.е у нас получаются следующие пары решений (х,у): (1,2), (1,-1), (2,1), (-1,1)
ответ: решение системы являются следующие пары решений (х,у): (1,2), (1,-1), (2,1), (-1,1)
Область определения функции определится по условиям, что знаменатель не может быть нулем, а под корнем не должно быть отрицательное число.
а) 16x²-49<>0
(4x-7)(4x+7)<>0
4x<>7
x<>7/4
4x<>-7
x<>-7/4
x ∈ (-∞;-7/4)U(-7/4; 7/4)U(7/4; +∞)
y ∈ (-∞; +∞)
б) x²+4x+3>0
найдем корни
x²+4x+3 = 0
По теореме Виета
х1 = -3
х2 = -1
(x+3)(x+1)>0
x+3>0, x>-3
x+1>0, x>-1
x > -1
x+3<0, x<-3
x+1<0, x<-1
x < -3
x ∈ (-∞; -3]U[-1; +∞)
Поскольку подразумевается арифметический корень, то у ∈ [0; +∞)
1)
Прибавим к 1му уравнению второе и получим:
2(х+y)=-12
x+y=-6
x=-6-y
Подставим допустим во 2 уравнение системы, получим
-6-y+y-(6+y)y=2
По теореме Виета корни будут: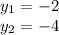
Находим х, получаем
ответ: решением системы являются пары чисел (х,у): (-4,-2), (-2, -4)
2)
Выразим из второго уравнения х, получим:
Теперь подставляем х=1 в 1 уравнение системы и получаем:
По теореме Виета:
Теперь рассмотрим случай, когда y=1, является ли он решением:
Подставляем в 1 и 2 уравнение системы и получаем:
По теореме Виета получаем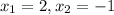
Т.е у нас получаются следующие пары решений (х,у): (1,2), (1,-1), (2,1), (-1,1)
ответ: решение системы являются следующие пары решений (х,у): (1,2), (1,-1), (2,1), (-1,1)
Область определения функции определится по условиям, что знаменатель не может быть нулем, а под корнем не должно быть отрицательное число.
а) 16x²-49<>0
(4x-7)(4x+7)<>0
4x<>7
x<>7/4
4x<>-7
x<>-7/4
x ∈ (-∞;-7/4)U(-7/4; 7/4)U(7/4; +∞)
y ∈ (-∞; +∞)
б) x²+4x+3>0
найдем корни
x²+4x+3 = 0
По теореме Виета
х1 = -3
х2 = -1
(x+3)(x+1)>0
x+3>0, x>-3
x+1>0, x>-1
x > -1
x+3<0, x<-3
x+1<0, x<-1
x < -3
x ∈ (-∞; -3]U[-1; +∞)
Поскольку подразумевается арифметический корень, то у ∈ [0; +∞)