Пусть одна сторона прямоугольника будет x см. Тогда другая сторона будет (x+7)см. Для того чтобы найти площадь прямоугольника, надо длину умножить на ширину. Так как площадь равна 44 квадратных сантиметров, то составляем уравнение:
x (x + 7) = 44
В результате его решения получается 4 и -11. Так как сторона прямоугольника не может быть отрицательным числом , то x=4 см, а другая сторона 4+7=11 см.
4. По теореме Виета
ах^2+bx+c
x1+x2=-b/a
x1*x2=c/a
x1=-6 по условию
-6*х2=-3( из формулы х1*х2=с/а)
х2=0.5
0.5-6=-b/2(из формулы х1+х2=-b/а)
b=-5.5*(-2)=11
5. 2
6. 186
В приведенном квадратном уравнении
по теореме Виета
где x{_1}, x{_2} - корни квадратного уравнения. Тогда
Найдем решения неравенства Ix-5I≤2; -2≤х-6≤2; 4≤х≤8- отрезок длиной 4
Найдем решения неравенства Ix-6I≥1
x-6≥1; х≥7 или х-6≤-1; х≤5; т.е. х∈(-∞;5]∪[7;8]
Из отрезка [4;8] выпадает только отрезок[5;7] длины 2
Используя геометрическое определение вероятности, найдем искомую вероятность, длина решений второго неравенства, которое находится в первом, составляет 2, это сумма длин отрезков [4;5] и [7;8], т.е. число благоприятствующих исходов равно 2, а общее число исходов 4, значит, вероятность равна 2/4=0.5
1. 1)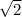
; 2) 1 и -7 ; 3)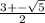 
2. https://ru-static.z-dn.net/files/d11/f7113b9eb1a0e17ab51d3c8219a1d33f.png
3. 4 см и 11 см
Пусть одна сторона прямоугольника будет x см. Тогда другая сторона будет (x+7)см. Для того чтобы найти площадь прямоугольника, надо длину умножить на ширину. Так как площадь равна 44 квадратных сантиметров, то составляем уравнение:
x (x + 7) = 44
В результате его решения получается 4 и -11. Так как сторона прямоугольника не может быть отрицательным числом , то x=4 см, а другая сторона 4+7=11 см.
4. По теореме Виета
ах^2+bx+c
x1+x2=-b/a
x1*x2=c/a
x1=-6 по условию
-6*х2=-3( из формулы х1*х2=с/а)
х2=0.5
0.5-6=-b/2(из формулы х1+х2=-b/а)
b=-5.5*(-2)=11
5. 2
6. 186
В приведенном квадратном уравнении
по теореме Виета
где x{_1}, x{_2} - корни квадратного уравнения. Тогда
для заданного уравнения
Объяснение:
Найдем решения неравенства Ix-5I≤2; -2≤х-6≤2; 4≤х≤8- отрезок длиной 4
Найдем решения неравенства Ix-6I≥1
x-6≥1; х≥7 или х-6≤-1; х≤5; т.е. х∈(-∞;5]∪[7;8]
Из отрезка [4;8] выпадает только отрезок[5;7] длины 2
Используя геометрическое определение вероятности, найдем искомую вероятность, длина решений второго неравенства, которое находится в первом, составляет 2, это сумма длин отрезков [4;5] и [7;8], т.е. число благоприятствующих исходов равно 2, а общее число исходов 4, значит, вероятность равна 2/4=0.5