перпендикуляры к заданным прямым будут описываться формулой соответственно:
так как коэффициенты при x одинаковы, сами прямые и их перпендикуляры параллельны, поэтому перпендикуляр проходящий через точку (2,1) будет проходит через центр окружности и пересекать точку касания первой прямой. уравнение этого перпендикуляра найдем подставив x и y
значит перпендикуляр пересекающий точки касания и центр окружности
точка касания первой прямой:
тогда центр окружности лежит посредине двух точек касания и получаем:
расстояние между этими точками равно двум радиусам, поэтому:
Объяснение:
заданная точка принадлежит прямой
перпендикуляры к заданным прямым будут описываться формулой соответственно:
так как коэффициенты при x одинаковы, сами прямые и их перпендикуляры параллельны, поэтому перпендикуляр проходящий через точку (2,1) будет проходит через центр окружности и пересекать точку касания первой прямой. уравнение этого перпендикуляра найдем подставив x и y
значит перпендикуляр пересекающий точки касания и центр окружности
точка касания первой прямой:
тогда центр окружности лежит посредине двух точек касания и получаем:
расстояние между этими точками равно двум радиусам, поэтому:
поэтому уравнение окружности:
ответ: для первого - квадрат со стороной 12.
Объяснение:
1) P = 2a + 2b, S = ab. Докажем, что прямоугольник имеет наибольшую площадь, если он является квадратом.
Пусть одна из сторон прямоугольника равна х. Тогда вторая равна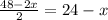 .
.
составим функцию: S(x) = x(24 - x) = 24x - x².
Найдем производную: S'(x) = 24 - 2x.
24 - 2х = 0; х = 12 - критическая точкаю
При переходе через точку х = 12 производная меняет знак с + на -. Следовательно, х - точка максимума, и в ней значение функции S(x) будет наибольшим.
Если а = 12 - первая сторона, то b = 24 - a = 12 - вторая сторона. Следовательно, искомый прямоугольник - квадрат со стороной 12 см.