1) sin a = √2/2; a1 = pi/4+2pi*k; cos a1 = √2/2 a2 = 3pi/4+2pi*k; cos a2 = -√2/2 cos(60 + a1) = cos 60*cos a1 - sin 60*sin a1 = = 1/2*√2/2 - √3/2*√2/2 = √2/4*(1 - √3) = -√2(√3 - 1)/4 cos(60 + a2) = cos 60*cos a2 - sin 60*sin a2 = = -1/2*√2/2 - √3/2*√2/2 = -√2/4*(1 + √3) = -√2(√3 + 1)/4
2) sin a = 2/3; cos b = -3/4; a ∈ (pi/2; pi); b ∈ (pi; 3pi/2) cos a < 0; sin^2 a = 4/9; cos^2 a = 1-4/9 = 5/9; cos a = -√5/3 sin b < 0; cos^2 b = 9/16; sin^2 b = 1-9/16 = 7/16; sin b = -√7/4 sin(a+b) = sin a*cos b + cos a*sin b = = 2/3*(-3/4) + (-√5/3)(-√7/4) = -6/12 + √35/12 = (√35 - 6)/12 cos(-b) = cos b = -3/4
x^2-6x+5=0. решим эти уравнения любым удобным , для меня это теорема обратная Т.Виета
произведение корней равно минус 10, а сумма равна 3, очевидно это 5 и минус 2, произведение корней равно 5, а сумма 6, очевидно это 5 и 1, и очень хорошо, что есть одинаковые корни. Мы имеем право записать квадратный трехчлен как a(x-x1)*(x-x2), где х1 и х2 это корни квадратного трехчлена, a - коэффициент перед старшей степенью. Тогда на х-5 можно сократить, окончательно получим.
a2 = 3pi/4+2pi*k; cos a2 = -√2/2
cos(60 + a1) = cos 60*cos a1 - sin 60*sin a1 =
= 1/2*√2/2 - √3/2*√2/2 = √2/4*(1 - √3) = -√2(√3 - 1)/4
cos(60 + a2) = cos 60*cos a2 - sin 60*sin a2 =
= -1/2*√2/2 - √3/2*√2/2 = -√2/4*(1 + √3) = -√2(√3 + 1)/4
2) sin a = 2/3; cos b = -3/4; a ∈ (pi/2; pi); b ∈ (pi; 3pi/2)
cos a < 0; sin^2 a = 4/9; cos^2 a = 1-4/9 = 5/9; cos a = -√5/3
sin b < 0; cos^2 b = 9/16; sin^2 b = 1-9/16 = 7/16; sin b = -√7/4
sin(a+b) = sin a*cos b + cos a*sin b =
= 2/3*(-3/4) + (-√5/3)(-√7/4) = -6/12 + √35/12 = (√35 - 6)/12
cos(-b) = cos b = -3/4
Объяснение:
Приравняем числитель и знаменатель к нулю, тогда
x^2-3x-10=0
x^2-6x+5=0. решим эти уравнения любым удобным , для меня это теорема обратная Т.Виета
произведение корней равно минус 10, а сумма равна 3, очевидно это 5 и минус 2, произведение корней равно 5, а сумма 6, очевидно это 5 и 1, и очень хорошо, что есть одинаковые корни. Мы имеем право записать квадратный трехчлен как a(x-x1)*(x-x2), где х1 и х2 это корни квадратного трехчлена, a - коэффициент перед старшей степенью. Тогда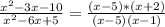
на х-5 можно сократить, окончательно получим.