4,8×10^7 т-в граммах
0,34×10^-4 мм- в километрах
8,8×10^4 км- в сантиметрах
0,53×10^-3 г - в тоннах
! ​

24 числа можно составить.

Из них на 2 делятся 4

На 4 делятся 2

на 11 делятся 4

Объяснение:

у нас есть 4-значное число. на 1 позицию мы можем поставить 4 числа, на 2-3, на 3-2, на 4-1. Перемножая все варианты получаем 24. Значит всего можно составить 24 числа. Из них на 2 деляться только те у кого а конце 2 или 4 то есть. то есть на 1 позицию можно поставить 2 числа (9 или 7) на вторую 1 число, на последние две тоже по  2  числа, получается 4 числа.

Аналогично для деления на 4 только на последние две позиции можно поставить обязательно 24, получаеся только 2 числа.

И для 11 есть 4 разных числа, где сумма на нечетных позициях = сумме на четных, то есть 4+7 и 2+9

1) для того чтобы функция была непрерывной, нужно чтобы пределы слева и справа в точках 0 и 1 были равны. Найдем их:

Так как 1≠-∞, то точка 0- это точка разрыва(второго рода).

Чтобы функция была неразрывной в точке 1, нужно чтобы предел от 3-ax^2 был равен 2, так как

При x=1 ⇒y=2.

Подставим координаты (1;2)  в формулу y=3-ax^2⇒2=3-а⇒а=1, то есть уравнение имеет вид y=3-x^2. Проверим это: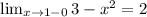

Действительно 2=2, значит функция не будет являться непрерывной в точке 1.

ответ: х=0 - точка разрыва. функция непрерывна в точке х=1 при а=1

2)  Аналогично:

3≠-1, значит -1- это точка разрыва.

В точке x=1 ⇒y=1. Подставим: 1=a*1⇒a=1.

Проверим: .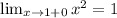

Так как точка  х=0 лежит в области определения функции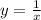 , а из ОДЗ следует что х≠0, то функция также будет прерываться в точке х=0

ответ: х=-1 - точка разрыва,  х=0- точка разрыва, функция будет непрерывна в точке х=1 при а=1