Алгебра: 4.Решите систему уравнений графическим :

#1. |2x-3|=3-2x, если х 3/2; |2x-3|=2x-3, если х≥3/2; |x-2|=2-x, если х 2; |x-2|=-2x, если х≥2; |x-6|=6-x, если х 6; |x-6|=x-6, если х≥6. Получаем три случая: 1) на множестве (-∞;3/2)U[2;6) получаем неравенство (2х-3)(х-2)≥(6-х)+2 2х²-3х-4х+6-6+х-2≥0 2х²-6х-2≥0 х²-3х-1≥0 D=9+4=13 C учётом (-∞;3/2)U[2;6) получим 2) на интервале 1,5≤х 2 получим неравенство (2х-3)(2-х)≥(6-х)+2 4х-6-2х²+3х-6+х-2≥0 -2х²+8х-14≥0 х²-4х+7≤0 D=16-28 0 решений нет 3) на интервале х≥6 получим неравенство (2х-3)(х-2)≥(х-6)+2...

4.Решите систему уравнений графическим :

Показать ответ

Ответ:

voenngti

02.04.2022 08:41

Букв у нас 10, 3 буквы А, по 2 буквы М и Т, и по одной Е, И и К.
На первую позицию можно ставить одну из десяти букв, на вторую, одну из девяти и т.д. Получим: 10!
Найдём количество которыми можно составить слово математика из данного набора букв при учёте позиции той или иной буквы.
Е, И и К могут занимать только одну позицию, а вот А, М и Т можно менять местами.
Для М и Т это будет 2! и 2!, для А – 3!
С учётом порядка позиции их будет: 1*1*1*2!*2!*3! = 24

Тогда вероятность (согласно классическому определению): $\frac{24}{10!} = \frac{1}{151200}$

Попробуем другой, более простой
Перестановки с повторением.
Всего у нас $\frac{(1 + 1 + 1 + 2 + 2 + 3)!}{3!*2!*2!} = \frac{10!}{3!*2!*2!}$
Перестановка с повторением, которая даёт нам слово "Математика" всего одна, потому мы получаем вероятность:
$\frac{1}{\frac{10!}{3!*2!*2!}} = \frac{3!*2!*2!}{10!} = \frac{24}{10!} = \frac{1}{151200}$

0,0(0 оценок)

Ответ:

иаешшвеэщк

26.08.2020 06:57

#1. |2x-3|=3-2x, если х<3/2; |2x-3|=2x-3, если х≥3/2;

|x-2|=2-x, если х<2; |x-2|=-2x, если х≥2;

|x-6|=6-x, если х<6; |x-6|=x-6, если х≥6.

Получаем три случая:

1) на множестве (-∞;3/2)U[2;6) получаем неравенство

(2х-3)(х-2)≥(6-х)+2

2х²-3х-4х+6-6+х-2≥0

2х²-6х-2≥0

х²-3х-1≥0

D=9+4=13

$(x-\frac{3-\sqrt{13}}{2})(x-\frac{3+\sqrt{13}}{2})\geq0 \\\ x \in (-\infty; \frac{3-\sqrt{13}}{2}] \cup [\frac{3+\sqrt{13}}{2}; +\infty)$

C учётом (-∞;3/2)U[2;6) получим $x \in (-\infty; \frac{3-\sqrt{13}}{2}]$

2) на интервале 1,5≤х<2 получим неравенство

(2х-3)(2-х)≥(6-х)+2

4х-6-2х²+3х-6+х-2≥0

-2х²+8х-14≥0

х²-4х+7≤0

D=16-28<0

решений нет

3) на интервале х≥6 получим неравенство

(2х-3)(х-2)≥(х-6)+2

2х²-3х-4х+6+6-х-2≥0

2х²-8х+10≥0

х²-4х+5≥0

D=16-20<0

решений нет

ответ: $x \in (-\infty; \frac{3-\sqrt{13}}{2}]$

#2. Пусть ∆АВС-прямоугольный треугольник с гипотенузой АВ, катетами АС и ВС.

По условию ВС+АВ=11, tg В = 3/4.

По определению тангенса острого угла прямоугольного треугольника

tg B=AC/BC=3/4 => 3BC=4AC =>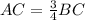 $AC=\frac{3}{4}BC$

По теореме Пифагора АВ² = АС² + ВС²

Пусть ВС=х, тогда АВ=11-х, АС=3х/4

$(11-x)^2=(\frac{3}{4}x)^2+x^2 \\\ 121-22x+x^2=\frac{9}{16}x^2+x^2 \\\ \frac{9}{16}x^2+22x-121=0 \\\ 9x^2+352x-1936=0\\\ \frac{D}{4}=176^2+9*1936=30976+17424=48400 \\\ x_1=-44,\ x_2=\frac{44}{9}=4\frac{8}{9} \\\ BC=4\frac{8}{9} \\\ AC=\frac{3}{4}*\frac{44}{9}=\frac{11}{3}=3\frac{2}{3}\\\ P_{ABC}=AB+BC+AC=11+AC=11+3\frac{2}{3}=14\frac{2}{3}$