Рассмотрим сначала вторую строку системы, так как с первой все предельно просто.
Здесь видим, что в числителе и знаменателе дроби присутствует восьмая степень. И если в числителе хотя бы угадываются два корня (-1 и 1), то со знаменателем все гораздо хуже. Поэтому первым делом попробуем с ним что-нибудь сделать. Будем выполнять преобразования по шагам.
Шаг 1 | Представим , как :
Шаг 2 | Заметим в получившемся выражении квадрат разности:
Шаг 3 | Вынесем за скобки:
Шаг 4 | Представим , как :
Шаг 5 | Заметим в получившемся выражении квадрат разности:
Шаг 6 (необязательный) | Раскроем скобки:
Получили, что .
Тогда исходной дроби равносильно:
Откуда следует, что .
Первое неравенство системы можно решить, просто раскрыв скобки, приведя подобные и разложив на множители.
В решении.
Объяснение:
Найти величину х из пропорции (1,25 * 14,9 + 0,75 * 1,1 + 14,9 * 0,75 + 1,1 * 1,25) : х = х : 0,125;
Упростить левую часть пропорции:
(1,25 * 14,9 + 0,75 * 1,1 + 14,9 * 0,75 + 1,1 * 1,25) : х =
= ((1,25 * 14,9) + (1,1 * 1,25)) + ((0,75 * 1,1) + (14,9 * 0,75)) : х =
= (1,25(14,9 + 1,1)) + (0,75(1,1 + 14,9)) : х =
= (1,25 * 16 + 0,75 * 16) : х =
= (16 * 2) : х = 32 : х;
Преобразованная пропорция:
32 : х = х : 0,125
Применить основное свойство пропорции (произведение крайних её членов равно произведению средних членов), решить уравнение и вычислить х:
х * х = 32 * 0,125
х² = 4
х = ±√4
х = ±2.
(см. объяснение)
Объяснение:
Рассмотрим сначала вторую строку системы, так как с первой все предельно просто.
Здесь видим, что в числителе и знаменателе дроби присутствует восьмая степень. И если в числителе хотя бы угадываются два корня (-1 и 1), то со знаменателем все гораздо хуже. Поэтому первым делом попробуем с ним что-нибудь сделать. Будем выполнять преобразования по шагам.
Шаг 1 | Представим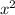 , как
, как 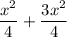 :
:
Шаг 2 | Заметим в получившемся выражении квадрат разности:
Шаг 3 | Вынесем за скобки:
за скобки:
Шаг 4 | Представим , как
, как 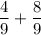 :
:
Шаг 5 | Заметим в получившемся выражении квадрат разности:
Шаг 6 (необязательный) | Раскроем скобки:
Получили, что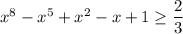 .
.
Тогда исходной дроби равносильно:
Откуда следует, что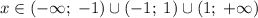 .
.
Первое неравенство системы можно решить, просто раскрыв скобки, приведя подобные и разложив на множители.
Тогда:
Найдем теперь пересечение:
Задание выполнено!