Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру уравнение в действительных корнях.
Рассмотрим функцию . Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию . Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
целые решения уравнения это делители свободного члена.
Можно подставлять все делители свободного члена, но нам нужно только 2, если уравнение 4 степение, и 3 если уравнение 5 степени(так как в этом случае мы разложим ее в таком виде (x-x1)(x-x2)(ax^2+bx+c)=0, а такое уравнение решить легко).
в первом это числа -2 и 3.
получаем x^4-x^3-5x^2-x-6=(x-3)(x+2)(x^2+1). теперь нужно каждый множитель приравнять нулю решить уравнения а потом обьеденить все корни:
а другие уравнения напиши в другой теме. по правилам сайта
Пользователи признают, что задания, которые содержат большое количество задач, требующих решения, должны быть разделены на два или несколько заданий и в таком виде добавлены в Сервис для других Пользователей. То есть в одном задании не может быть несколько задач.
, проходящие через точки, где график пересекает оси координат, пaраллельны.
Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру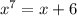
уравнение в действительных корнях.
Рассмотрим функцию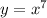
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию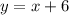
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение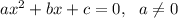
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
целые решения уравнения это делители свободного члена.
Можно подставлять все делители свободного члена, но нам нужно только 2, если уравнение 4 степение, и 3 если уравнение 5 степени(так как в этом случае мы разложим ее в таком виде (x-x1)(x-x2)(ax^2+bx+c)=0, а такое уравнение решить легко).
в первом это числа -2 и 3.
получаем x^4-x^3-5x^2-x-6=(x-3)(x+2)(x^2+1). теперь нужно каждый множитель приравнять нулю решить уравнения а потом обьеденить все корни:
x-3=0 => x=3; x+2=0 => x=-2; x^2+1=0 нет корней. ответ: -2; 3
а другие уравнения напиши в другой теме. по правилам сайта
Пользователи признают, что задания, которые содержат большое количество задач, требующих решения, должны быть разделены на два или несколько заданий и в таком виде добавлены в Сервис для других Пользователей. То есть в одном задании не может быть несколько задач.