Попробуем угадать исходную функцию. Рассмотрим слагаемое 21x. Пусть в исходной функции перед x стоял коэффициент C₁. Тогда 2C₁x - (-C₁x) = 3C₁x = 21x ⇒ C₁ = 7. Рассмотрим модули. Заметим, что |-x + a - 5| = |x - a + 5|. Пусть в исходной функции содержалось выражение C₂|x + a - 5| + C₃|x - a + 5|. Тогда для полученных коэффициентов составим систему:
Свободный член не зависит от x, поэтому если в исходной функции было выражение C₄(-8a + 28), то в выражении оно равно 2C₄(-8a + 28) - C₄(-8a + 28) = C₄(-8a + 28) = -8a + 28 ⇒ C₄ = 1.
Значит, . График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
Если верна пропорция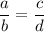 , то по основному свойству пропорции произведение крайних членов равно произведению средних членов:
, то по основному свойству пропорции произведение крайних членов равно произведению средних членов:
Рассмотрим пропорцию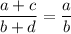 . Проверим, равно ли произведение крайних и произведение средних членов:
. Проверим, равно ли произведение крайних и произведение средних членов:
Слагаемое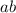 взаимно уничтожается.
взаимно уничтожается.
Это равенство верно, так как оно получено из исходной верной пропорции.
Рассмотрим пропорцию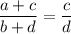 . Проверим, равно ли произведение крайних и произведение средних членов:
. Проверим, равно ли произведение крайних и произведение средних членов:
Слагаемое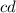 взаимно уничтожается.
взаимно уничтожается.
Это равенство также верно, так как оно получено из исходной верной пропорции.
17
Объяснение:
Попробуем угадать исходную функцию. Рассмотрим слагаемое 21x. Пусть в исходной функции перед x стоял коэффициент C₁. Тогда 2C₁x - (-C₁x) = 3C₁x = 21x ⇒ C₁ = 7. Рассмотрим модули. Заметим, что |-x + a - 5| = |x - a + 5|. Пусть в исходной функции содержалось выражение C₂|x + a - 5| + C₃|x - a + 5|. Тогда для полученных коэффициентов составим систему:
Свободный член не зависит от x, поэтому если в исходной функции было выражение C₄(-8a + 28), то в выражении оно равно 2C₄(-8a + 28) - C₄(-8a + 28) = C₄(-8a + 28) = -8a + 28 ⇒ C₄ = 1.
Значит,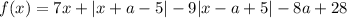 . График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
. График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
Наибольшее значение параметра — 17.