(√5÷3) -1/3(степень) и (√5÷3) -1/2(степень)
Сравнить
как сравнивать числа с отриц степенями? Заранее спс

x^2 - 3x + 2 = (x - 1)(x - 2) < 0

Решением этого неравенства является промежуток (1, 2)

Разложим на множители левую часть второго неравенства:

ax^2 - (3a + 1)x + 3 = (ax^2 - x) - (3ax - 3) = x(ax - 1) - 3(ax - 1) = (x - 3)(ax - 1) = a(x - 3)(x - 1/a)

Возможны 5 вариантов.

1) a > 1/3. Тогда решение неравенства – промежуток (1/a, 3). Нужно, чтобы промежуток (1, 2) полностью содержался в нём, так будет, если 1/a < 1. Объединяем с условием a > 1/3 и получаем часть ответа: a > 1.

2) a = 1/3. У второго неравенства нет решений.

3) 0 < a < 1/3. Решение неравенства – промежуток (3, 1/a); такой промежуток никогда не содержит (1, 2).

4) a = 0. Второе неравенство превращается в 3 - x < 0, x > 3. Не подходит.

5) a < 0. Решение второго неравенства – промежуток (1/a, 3), при этом 1/a < 0. Подходит.

ответ.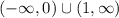

х^2 - 3x + 2 < 0
(x-1)(x-2)< 0
x (1;2)
ax^2 - (3a + 1)x + 3 < 0

D=(3a+1)^2-12a=9a^2+6a+1-12a=9a^2-6a+1.
что бы получились 2 корня 9a^2-6a+1 должно быть  >0
9a^2-6a+1>0/
(3a-1)^2 - подный квадрат, всегда положителен, и равен нулю когда а =1/3.
тогда что бы корней было 2 а должна быть не равна 1/3.

корни 
х12= ((3а+1)+-(3а-1))/2а
x1=3. x2=1/a.
решение уравнения 1 (1;2)
должно удовлетворять и решению 2 уравнения, тогда верхняя граница у второго уравнения х=3, нижняя - х=1/а, 
0<1/а <3
1/3<a<+бесконечность
ответ в круглых скобках. т к 1/3 не входит в одз а